Математика: Теория чисел: Длинная арифметика.

Исходники - реализация основных операций стандартным образом и (!) алгоритма Шенхаге-Штрассена вместе с БПФ.

Способ представления зависит от наших целей. Обычно, большое число N представляется в виде

B - основание системы счисления, в которой записывается число. Все x_i - стандартные числа /long или double, например/ и 0 <= x_i < B

При записи дробных чисел второй способ легче, однако введение e - целой степени, в зависимости от которой мы ставим на нужный знак 'запятую' в обычном числе y, сильно осложняет операции.

Знак числа либо хранится отдельно, либо все x_i < 0.

Основание B обычно зависит от максимального размера базового типа данных на компьютере, и выбирается, исходя из следующих соображений:

• Основание B подходить под один из базовых типов данных
  
  
• B должно быть как можно больше, чтобы уменьшить размер представления длинного числа и увеличить скорость операций с ними, но достаточно малого размера, чтобы все операции с коэффициентами использовали базовый тип данных.
  
  
• Для удобства можно выбрать B как степень 10 ( вывод информации, отладка ). B - степень двойки позволяет проводить быстрые операции на низком уровне. Нужно иметь в виду, что быстрый переход от основания B = 2^m к B = 10ⁿ для больших чисел реализовать весьма и весьма непросто.
  Некоторые задачи, например определение простоты, могут использовать реализацию при B = 2^m, так как вывод - логическое ДА или НЕТ.

Для коэффициентов x_i естественно выбрать тип long (в Cи). Однако, long обычно занимает 32 бита, а использование double (Си - обычно 53 бита) дает возможность получить большее основание.

Кроме того, некоторые процессоры ( напр. pentium ) специально оптимизированы для операций с плавающей точкой, поэтому лучше выбирать double.

typedef double Real;
typedef struct BigIntTag {
  Real * Coef;
  long Size, SizeMax;
} BigInt;

#define BASE 10000.
#define invBASE 0.0001   //   B-1
#define NBDEC_BASE 4     //  Число знаков в B

2.1   Преобразование к каноническому виду

Переход от неканонического представления

Начиная с i = 0, делим с остатком x_i на B и осуществляем перенос на x_i+1.

void UpdateBigInt(BigInt * A)
{
  long i;
  Real carry=0., x;

  for (i=0; i<A->Size; i++) {
    x = A->Coef[i] + carry;
    carry = floor(x*invBASE);
    A->Coef[i] = x-carry*BASE;
  }
  if (carry!=0) {
    while (carry!=0.) {
      x = carry;
      carry = floor(x*invBASE);
      A->Coef[i] = x-carry*BASE;
      i++;
      A->Size=i;
    }
    if (A->Size > A->SizeMax) {
      printf("Error in UpdateBigInt, Size > SizeMax\n");
    }
  }
  else {
    while (i>0 && A->Coef[i-1]==0.) i--;
    A->Size=i;
  }
}

2.2   Сумма и разность.

Cкладываем коэффициенты и осуществляем преобразование к каноническому виду при сложении, аналогично - разность.

/*
 *  C = A + B
 */
void AddBigInt(BigInt * A, BigInt * B, BigInt * C)
{
  long i;

  if (A->Size < B->Size) {
    AddBigInt(B,A,C);
    return;
  }
  /* We now have B->Size < A->Size */
  for (i=0; i < B->Size; i++)
    C->Coef[i] = A->Coef[i] + B->Coef[i];
  for (; i < A->Size; i++) 
    C->Coef[i] = A->Coef[i];

  C->Size = A->Size;
  UpdateBigInt(C);
}

2.3   Умножение на малое целое.

Пусть q - такое целое, что qB подходит под тип данных коэффициентов. Тогда произведение x на q получаем, умножая каждое x_i на q и осуществляя перенос с i = 0 и далее.

2.4   Деление на малое целое.

Начиная с i = n, делим каждое x_i на q и осуществляем перенос, умноженный на B в x_i-1 и так далее.

2.5   Обычное перемножение двух длинных чисел.

Пусть даны 2 длинных числа в канонической форме:

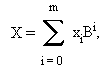
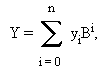
Длинное число Z = X*Y может быть вычислено по формуле:

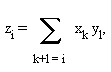
Архив статей.

• Generalized Arithmetic in C++
Метод представления длинных чисел, удобный для программирования. Безразлично, что представлено: десятичные или обычные дроби, челые числа, комплексные или полиномы.

Вверх по странице, к оглавлению и навигации