Математика: Теория чисел: Длинная арифметика: Метод Шенхаге-Штрассена.

Быстрое умножение.

Стандартные алгоритмы сложения, вычитания и умножения/деления на малое целое дают сложность O(n). Умножение же требует O(n²) для двух чисел размера n. Это намного больше и сильно тормозит программы.

Для ускорения этого процесса существует метод Карацубы, однако из-за сложности в реализации его практически никто не использует, применяя асимптотически лучший алгоритм Шенхаге-Штрассена.

Благодаря Быстрому Преобразованию Фурье можно осуществить умножение за O( n log(n) log(log(n)) операций, что практически равно O(n log(n)): log(log(n)) возрастает чрезвычайно медленно.

   Введение.

Два больших числа X и Y размера не больше n-1 могут, как мы говорили, быть записаны в виде X=P(B), Y=Q(B), где B - основание, а P и Q - два полинома.

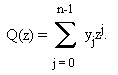
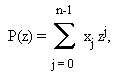
Обозначая R(z) произведение P(z)*Q(z), имеем X*Y = R(B), и, после преобразования коэффициентов, мы получаем произведение X*Y.

Таким образом, мы пришли к задаче о перемножении двух полиномов степени < n.

Полином степени < m однозначно определен своими значениями в m различных точках (и может быть вычислен, например, интерполяцией по Лагранжу ). Так что для получения R(z) = P(z)Q(z), достаточно вычислить значения R(w_k) в 2n различных точках w_k. А это можно сделать, вычислив значения P(w_k) и Q(w_k).

Идея Быстрого Преобразования Фурье - выбрать для w_k комплексные корни из 1.

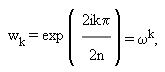
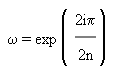
Такой выбор w_k обладает двумя свойствами:

• Наборы значений (P(w₀), ... ,P(w_2n-1)) и (Q(w₀), ... ,Q(w_2n-1)) могут быть вычислены за O(n logn).
  
  
• По значениям R(w_k) для i = 0, ... ,2n-1, полином R(z) может быть восстановлен за O(n logn).

Последнее замечание следует из того, что k-й коэффициент r_k R(z) удовлетворяет равенствам

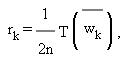
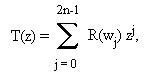
На языке математики, коэффициенты R(z) получаются из сопряженного преобразования Фурье от T(z).

1.1   Преобразование Фурье.

Итак, благодаря предыдущим рассуждениям, у нас осталась лишь одна проблема.

Дана последовательность A = (a₀, a₁, ... , a_2n-1), требуется вычислить ее преобразование Фурье

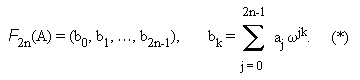
И, далее, восстановить R(z) по Фурье-преобразованию его коэффициентов R( w^j ), записанных в виде:

где сопряженное преобразование Фурье

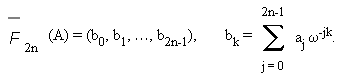
1.2   Быстое Преобразование Фурье.

Быстое Преобразование Фурье (БПФ) - способ вычислить преобразование последовательности A за время O(n logn), вместо обычного O(n²) в случае, если n - степень 2.

Используя запись (*), запишем

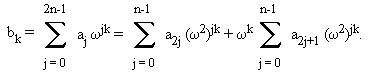
То есть для того, чтобы вычислить коэффициенты b_k F_2n(A), нужно проделать следующие шаги:

• Определить две подпоследовательности размера n:

  A0 = (a0, a2, ... , a2n-2),    и    A1 = (a1,a3, ... ,a2n-1).

• Вычислить преобразования Фурье

  C = Fn(A0) = (c0,c1, ... ,cn-1)     and   D = Fn(A1) = (d0,d1, ... ,dn-1).

• Вывести из этого преобразование Фурье B = (b₀, ... ,b_2n-1) = F_2n(A) по формулам:

  bk = ck + wk dk,    bn+k = ck - wk dk,      0 <= k < n.

Таким образом, стоимость T(2n) вычисления F_2n(A) через БПФ удовлетворяет равенству T(2n) = 2T(n) + O(n). Когда n - степень двух, можно сделать процесс рекурсивным, получив T(n) = O(n logn). Для сопряженного преобразования Фурье алгоритм, естественно, аналогичен.

2   Умножение с использованием БПФ.

2.1   Алгоритм.

А теперь - формальный алгоритм, как умножать длинные числа через БПФ.

Пусть n - степень двух. Два больших числа X и Y имеют меньше n коэффициентов.

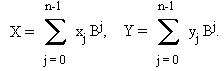
Для вычисления Z = XY за время O(nlog(n)), сделайте следующее:

• Методом БПФ вычислите преобразование Фурье X^* размера 2n последовательности (x_j) :

  X* = (x0*,x1*, ... ,x2n-1*) = F2n(x0,x1, ... ,xn-1,0, ... ,0)

• Также вычислите преобразование Y^* от (y_j) :

  Y* = (y0*,y1*, ... ,y2n-1*) = F2n(y0,y1, ... ,yn-1,0, ... ,0).

• Вычислить произведение X^* на Y^* в Z^*

  Z* = (z0*,z1*, ... ,z2n-1*),      zi* = xi* yi*.

• Вычислить обратное преобразование Фурье Z от Z^* (используя сопряженное БПФ)

  Z = (z0,z1, ... ,z2n-1) = 1 2n F   2n  (Z*).

• Тогда, после преобразования к каноническому виду коэффициентов z_i, число
  
  
  

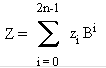
  равно произведению X на Y.

Заметим, что X^* - преобразование Фурье последовательности, образованной с n добавленными к x₀, ... ,x_n-1 нулями. Это же верно и в отношении Y^*.

Алгоритм состоит из вычисления двух БПФ размера 2n, 2n произведений базовых типов данных (их сложность пренебрежимо мала), и одного обратного БПФ размера 2n. Итого 3 БПФ.

Для возведения в квадрат числа размера n, требуется лишь одно прямое БПФ, а значит сложность возведения в квадрат - 2 БПФ..

2.2   Вычислительные ошибки.

На практике, нам понадобится использовать базовый тип double в C для операций с плавающей точкой, появляющихся в ходе преобразования Фурье. В ходе вычислений могут появиться ошибки округления. Если они достаточно малы, то ими можно пренебречь.

Для окончательных значений z_i после обратного преобразования Фурье, которые должны быть целыми, возьмем ближайшее целое значение. Дробное будет ликвидировано как ошибка.

Можно доказать, что верхняя грань вычислительных ошибок a для z_i после БПФ

где e ~= 1.e-16 - машинная точность операций с i double.

Однако это - худший случай, который весьма маловероятен. На практике, ошибки довольно малы, и выполняется ограничение a = O(nB²e).

Чтобы правильно вывести значение z_i, взяв ближайшее целое, нам требуется a < 0.5, а еще лучше а < 0.25 !.

Выбор основания B из 3-4 цифр обычно дает желаемую точность при перемножении больших целых чисел.

3.    Реализация.

Простейшую реализацию БПФ написать довольно легко. Чтобы сделать ее действительно эффективной, нужно использовать то, что x^*_2n-k - сопряженное к x^*_k (hermitian FFT), чтобы не вычислять одно и тоже дважды и хранить минимум информации. Эта задача, вкупе с максимально эффективным хранением данных без операций копирования, гораздо сложнее.

Аккуратно запрограмированный алгоритм БПФ делает метод Шенхаге-Штрассена более эффективным, нежели любой другой алгоритм, при числах с 10000 знаками и более. А для меньших чисел пойдет и стандартный O(n²) ;-))

Исходники:

Вверх по странице, к оглавлению и навигации.