Поиск по сайту.

Другие алгоритмы.

Графика и обработка изображений. Фракталы.

Алгоpитмы двумерного отсечения.

Алгоритм Кируса-Бека.

Есть область ( видимая или невидимая ) и через неё проходит отрезок.

Исходные данные : выпуклая область отсечения.

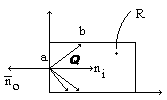( рис. 1 )

Алгоритм Кируса - Бека работает только с выпуклыми областями.

Используем понятие - внутренняя нормаль, т.е. если любая (o) принадлежит ребру, (o) b в другой границе окна, то произведение м.б. любым внутренним вектором на внутренней нормали, проведенной из этой же (o), будет положительно т.к. любой угол < 90 градусов.

Если применить к внешней нормали, то

Произведение вектора на внешнюю нормаль будет всегда отрицательным.

Пусть есть отрезок ( P1, P2) ( рис.2 ) , представим его в параметрическом виде.

P(t) = P1 + ( P2 - P1 ) t , где t - параметр ( расстояние от начальной (o) до конечной (o))

Пусть какая-то точка F будет являться граничной точкой окна, тогда из вышесказанного мы можем сказать, что для любого отрезка ( P1, P2 ) справедливо следующие :

1. П[ P(t) - F ] < 0, когда [ P(t) - F ] направлен во вне R.
2. П[ P(t) - F ] = 0 -- [P(t) - F] принадлежит плоскости, проходящей через точку F и перпендикулярной нормали.
3. П[ P(t) - F ] > 0, когда [ P(t) - F ] направлен во внутрь R.

Выводы:

1. Бесконечная прямая пересекает замкнутую выпуклую область ровно в двух точках и это справедливо для n - мерного пространства.

2. Пусть эти 2 точки не принадлежит одному ребру или граничной плоскости, тогда выражение n[ P(t) - F ] = 0 будет иметь только одно решение.

3. Если точка F принадлежит ребру для которого вектор n внутренняя нормаль, то точка P(t) будет являться точкой пересечения данного отрезка с указанной граничной плоскостью.

Пример 1. Частично видимый отрезок.

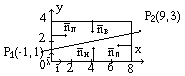(рис.2)

Уравнение прямой P1P2 = 0,2( X - 6 ).

Запишем этот отрезок в параметрическом виде т.е.:

P(1) = [-1, 1] + [10, 2] t = (10t - 1) i + (2t + 1 ) j, 0 <= t <= 1,

i, j - нормальные единичные вектора.

Зададим в окне нормали

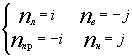
а) Для удобства вычисления допустим, что (o) F = (0,0), тогда [ P(t) - F ] = (10t - 1 )i + (2t + 1)j.

Рассмотрим произведение nл[ P(t) - F] = 10t - 1 = 0 t = 0,1.

Подставляем t в наше параметрическое уравнение, т.е. P(0,1) = [-1,1] + [10,2] 0,1 = [0,1 , 2].

б) Берем точку F = (8,4).

Опять находим вектор.

[ P(t) - F ] = ( 10t - 0)i + ( 2t - 3 )j
nn[ P(t) - i ] = 10t -8 = 0 t = 0,9
nн[ P(t) - F ] = 2t + 1 = 0 t = - Ѕ - отвергаем
nв[ P(t) - F ] = - ( 2t -3 ) = 0 t = 3/2 - отвергаем

Для nн, nв параметр t не лежит в заданной области. Эти точки t нам не нужны.

Подставляем t = 0,9 в параметрическое уравнение P(0,9) = [ 8, 2,8]

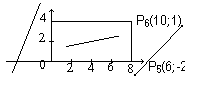Отсюда следует, что видимый участок лежит в пределах 0,1Пример 2. Нетривиальный невидимый отрезок.

(рис. 3)
а) Допускаем, что пересекается с какой то стороной.
б) Перемножаем на все нормали.
в) Приравниваем n = 0.
г) Смотрим так это или не так.
Составляем параметрическое уравнение.
P(t) = [ 6, -2] + [ 4, 3]t

P5P6 не является тривиально невидимым.

л -3/2 = t; п 1/2 = t; н 2/3 = t; в 2 = t; - не верно => важна ориентация отрезка.

Если взять ориентацию отрезка P5 => P6, то получается что отрезок пересекает сначала правое, а затем нижнее ребро, но такого быть не может => такие параметры не подходят.

Из приведенного выше примера следует, что для правильного подбора параметров, нужно учитывать ориентацию отрезка.

Формализованный алгоритм Кируса-Бука.

Мы говорим, что :

1. Параметрическое уравнение отрезка имеет вид:

P(t) = P1 + ( P2 - P1 )t , 0 <= t <= 1.

2. ni[ P(t) - F ] , i = 1,2,3 ... - кол-во ребер. Это произведение либо > 0, либо < 0, либо = 0.

3. Подставляем первое уравнение во второе, получаем условие пересечения отрезка с границей области. ni [ P1 + ( P2 - P2 )t - Fi ] = 0

4. ni [ Pi - Fi ] + ni[ P2 - P1 ]t = 0.

Условие пересечения отрезка с граничной плоскостью. Вводим обозначения.

D - директриса
D = P2 - P1
Wi = P1 - Fi

Тогда получается п. 5.

5. t( ni D) + Wi ni = 0; t = (- Wi ni ) / ( ni * D ) , i = 1,2,3

Выражение

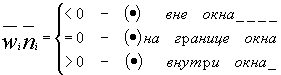
В случае, когда имеется больше двух решений, они разбиваются на две группы нижнею и верхнею. Находят наибольшее из нижних и наименьшее из верхних.

6 D * ni > 0, то найденное значение t рассматривается как возможный нижний предел. D * ni < 0, - возможный верхний предел.

Разбиение невыпуклых многоугольников.

Пусть область невыпуклая :

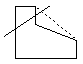
дополнить область, или разбить ее на выпуклые области.

Факт выпуклости или вогнутости определяется путем векторного произведения всех смежных сторон.

Рассмотрим знаки :

  • 1. все знаки равны нулю - многоугольник вырождается в отрезок;
  • 2. есть и "+" и "-" - многоугольник не выпуклый;
  • 3. все неотрицательные - многоугольник выпуклый и все нормали ориентированны влево от контура;
  • 4. все неположительные - многоугольник выпуклый и все нормали ориентированны вправо от контура.

Вычисление нормалей :

Одна вершина выбирается как базовая и все векторные произведения вычисляются относительно ее.

(vx1vy2 - vy1vx2)k - векторное произведение v1,v2.

n*vE = (nx*i + nyj)(vEx*i + vEx*j) = nxvEx + nyvEy + 0;

nxvEx = -hyvEy {ny = 1}

nx = -(vEy / vEx)*i + j

vi-1 и vi - вершины

vi-1 * vi > 0, то n - внутренняя нормаль, иначе - внешняя.

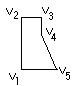
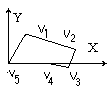
  • 1. перенос начала координат в точку v1;
  • 2. начинаем вращать фигуру так, чтобы любое ребро лежало на оси X
  • 3. если Y вершины меньше нуля, то фигура невыпуклая и она отсекается соседями.

Последовательное осечение многоугольников. Алгоритм Сазермана - Ходтмена.

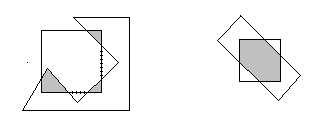
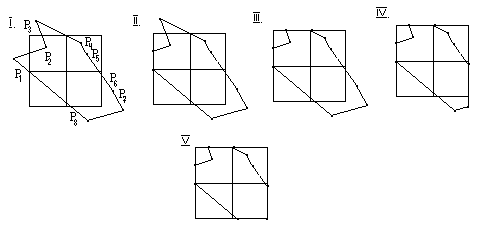
Суть: Произвести отсечение относительно одной прямой. Отсекается все что невидимо. Исходный многоугольник задается списком вершин (P1, ... , Pn). Порождается список ребер (P1P2, ... , Pn-1 Pn, PnP1). Нахождение точки Q8 стало тривиальным.

Исходный многоугольник может быть любым, а отсекающий должен быть всегда выпуклым. Порядок отсечения не имеет принципиального значения. Результат работы алгоритма - список вершин многоугольника, который лежит по видимую сторону отсекающей плоскости.

Возможны четыре варианта положения отсекателя и многоугольника :

  • 1.полная видимость : Результат - точка P(полная видимость). Точка S в результирующий список не заносится.
  • 2. полная невидимость : Результат - точек нет.
  • 3. выход из области видимости : Результат - точка I.
  • 4. вход в видимую область : Результат - точки I,P.

Для первой вершины достаточно определить, является ли она видимой, если да, то она попадает в результирующий список и является начальной точкой S; если нет, то она не попадает результирующий список, но становится точкой S.

Последнее ребро PnP1: точку P1 рассматривают как точку F и ребро PnP1 рассматривают как обычное ребро PnF.

Плохая особенность алгоритма: ложные границы.

Пример возникновения ложных границ.

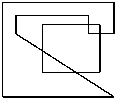
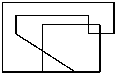
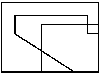
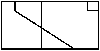
Невыпуклые отсекающие области. Алгоритм Вейлера - Айдертона.

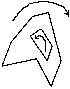
Внешняя граница обходится по часовой стрелке, а внутренняя - против.

При обходе вершин многоугольника в порядке их следования в соотв. списке внутр. обл. будут расположены справа от границы.

Если границы пересекаются, то точки пересечения образуют пары. Одно пересечение - когда ребро обр. многоугольника входит внутрь отсекателя, а другое - когда оно выходит из отсекателя.

Основная идея :

Точки пересечения будут делиться на входные и выходные. Алгоритм начинается с точки пересечения входного типа, затем он прослеживает внешнюю границу по часовой стрелке, до тех пор пока не обнаружит еще одно пересечение с отсекающим многоугольником (отсекателем) .

В точке последнего пересечения производится поворот направо, далее прослеживается внешняя граница отсекателя по часовой стрелке, до тех пор пока не обнаружится ее пересечение с исходным (обрабатываемым) многоугольником и так далее пока не встретится начальная вершина.

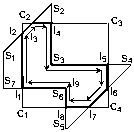
  • C1 C2 C3 C4 - отсекатель
  • S - исходный многоугольник
  • I - точки пересечения

Вершина отсекателя

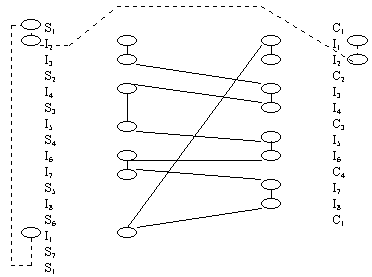
I2 I3 I4 S3 I5 I6 I7 I8 S6 I1 I2 - Результат внутреннего отсечения

Отсечение происходит таким образом, что число многоугольников минимально.