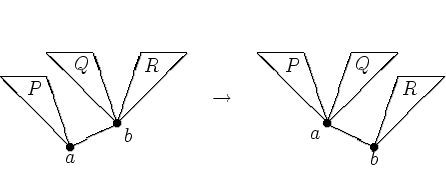 Пусть вершина a имеет правого сына b . Обозначим через P
левое поддерево вершины a , через Q и R -- левое и правое
поддеревья вершины b .
Упорядоченность дерева требует, чтобы
Пусть вершина a имеет правого сына b . Обозначим через P
левое поддерево вершины a , через Q и R -- левое и правое
поддеревья вершины b .
Упорядоченность дерева требует, чтобы Мы хотим восстанавливать сбалансированность дерева после
включения и удаления элементов. Для этого необходимы какие-то
преобразования дерева, не меняющие множества пометок на его
вершинах и не нарушающие упорядоченности, но способствующие
лучшей сбалансированности. Опишем несколько таких
преобразований.
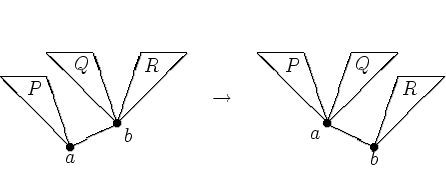 Пусть вершина a имеет правого сына b . Обозначим через P
левое поддерево вершины a , через Q и R -- левое и правое
поддеревья вершины b .
Упорядоченность дерева требует, чтобы
Пусть вершина a имеет правого сына b . Обозначим через P
левое поддерево вершины a , через Q и R -- левое и правое
поддеревья вершины b .
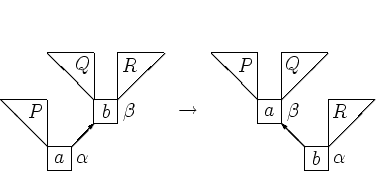
Упорядоченность дерева требует, чтобы ![]() (точнее следовало бы сказать << любая пометка на P меньше пометки
на a >>, << пометка на a меньше любой пометки на Q >> и т.д., но мы
позволим себе этого не делать). Точно того же требует
упорядоченность дерева с корнем b , его левым сыном a , в котором
P и Q -- левое и правое поддеревья a , R -- правое поддерево b .
Поэтому первое дерево можно преобразовать во второе, не нарушая
упорядоченности. Такое преобразование назовем малым правым
вращением (правым -- поскольку существует симметричное, левое,
малым -- поскольку есть и большое, которое мы сейчас опишем).
(точнее следовало бы сказать << любая пометка на P меньше пометки
на a >>, << пометка на a меньше любой пометки на Q >> и т.д., но мы
позволим себе этого не делать). Точно того же требует
упорядоченность дерева с корнем b , его левым сыном a , в котором
P и Q -- левое и правое поддеревья a , R -- правое поддерево b .
Поэтому первое дерево можно преобразовать во второе, не нарушая
упорядоченности. Такое преобразование назовем малым правым
вращением (правым -- поскольку существует симметричное, левое,
малым -- поскольку есть и большое, которое мы сейчас опишем).
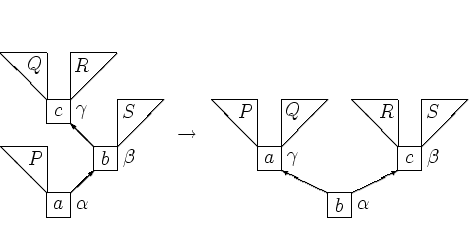
Пусть b -- правый сын a , c -- левый сын b , P --
левое поддерево
a , Q и R -- левое и правое поддеревья c , S
-- правое поддерево b .
Тогда ![]() .
.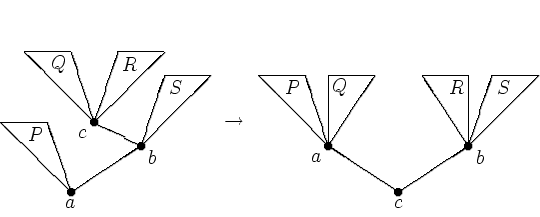 Такой же порядок соответствует дереву с корнем c , имеющим левого
сына a и правого сына b , для которого P и Q -- поддеревья вершины
a , а R и S -- поддеревья вершины b . Соответствующее
преобразование будем называть большим правым вращением.
(Аналогично определяется симметричное ему большое левое
вращение.)
Такой же порядок соответствует дереву с корнем c , имеющим левого
сына a и правого сына b , для которого P и Q -- поддеревья вершины
a , а R и S -- поддеревья вершины b . Соответствующее
преобразование будем называть большим правым вращением.
(Аналогично определяется симметричное ему большое левое
вращение.)
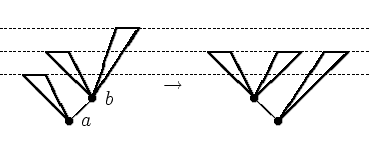
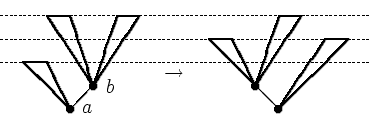
![]() 12.2.3. Дано дерево, сбалансированное всюду, кроме корня, в
котором разница высот равна 2 (т.е. левое и правое поддеревья
корня сбалансированы и их высоты отличаются на 2). Доказать, что
оно может быть превращено в сбалансированное одним из четырех
описанных преобразований, причем высота его останется прежней
или уменьшится на 1.
12.2.3. Дано дерево, сбалансированное всюду, кроме корня, в
котором разница высот равна 2 (т.е. левое и правое поддеревья
корня сбалансированы и их высоты отличаются на 2). Доказать, что
оно может быть превращено в сбалансированное одним из четырех
описанных преобразований, причем высота его останется прежней
или уменьшится на 1.
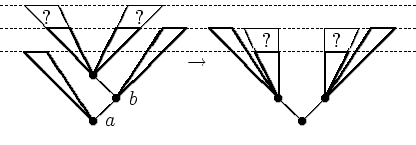
![]() 12.2.4. В сбалансированное дерево добавили или из него
удалили лист. Доказать, что можно восстановить
сбалансированность с помощью нескольких вращений, причем их
число не больше высоты дерева.
12.2.4. В сбалансированное дерево добавили или из него
удалили лист. Доказать, что можно восстановить
сбалансированность с помощью нескольких вращений, причем их
число не больше высоты дерева.
Лемма. Если в сбалансированном дереве X одно из его поддеревьев Y заменили на сбалансированное дерево Z , причем высота Z отличается от высоты Y не более чем на 1 , то полученное такой << прививкой>> дерево можно превратить в сбалансированное вращениями (причем количество вращений не превосходит высоты, на которой делается прививка).
Частным случаем прививки является замена пустого поддерева на лист или наоборот, так что достаточно доказать эту лемму.
Доказательство леммы. Индукция по высоте, на которой делается прививка. Если она происходит в корне (заменяется все дерево целиком), то все очевидно (<< привой>> сбалансирован по условию). Пусть заменяется некоторое поддерево, например, левое поддерево некоторой вершины x . Возможны два случая.
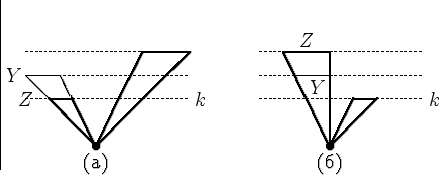
![]() 12.2.5. Составить программы добавления и удаления элементов,
сохраняющие сбалансированность. Число действий не должно
превосходить
12.2.5. Составить программы добавления и удаления элементов,
сохраняющие сбалансированность. Число действий не должно
превосходить ![]() . Разрешается
хранить в вершинах дерева дополнительную информацию, необходимую
при балансировке.
. Разрешается
хранить в вершинах дерева дополнительную информацию, необходимую
при балансировке.
![\begin{eqnarray*}
{\hbox{\tt diff [i]}}& = &\hbox{(высота правого поддерева верш...
... &\qquad \hbox{(высота левого поддерева вершины {\hbox{\tt i}}).}\end{eqnarray*}](img543.gif) Нам потребуются четыре процедуры, соответствующие большим и
малым правым и левым вращениями. Но вначале два замечания.
(1) Нам нужно, чтобы при вращении поддерева номер его корня
не менялся. (В противном случае потребовалось бы корректировать
информацию в отце корня, что нежелательно.) Этого можно достичь,
так как номера вершин дерева можно выбирать независимо от их
значений. (На картинках номер указан сбоку от вершины, а
значение -- внутри.)
Нам потребуются четыре процедуры, соответствующие большим и
малым правым и левым вращениями. Но вначале два замечания.
(1) Нам нужно, чтобы при вращении поддерева номер его корня
не менялся. (В противном случае потребовалось бы корректировать
информацию в отце корня, что нежелательно.) Этого можно достичь,
так как номера вершин дерева можно выбирать независимо от их
значений. (На картинках номер указан сбоку от вершины, а
значение -- внутри.)
 (2) После преобразований мы должны также изменить
соответственно значения в массиве diff. Для этого
достаточно знать высоты деревьев
(2) После преобразований мы должны также изменить
соответственно значения в массиве diff. Для этого
достаточно знать высоты деревьев Вот процедуры вращений:
procedure SR (a:integer); {малое правое вращение с корнем a}
| var b: 1..n; val_a,val_b: T; h_P,h_Q,h_R: integer;
begin
| b := right [a]; {b <> null}
| val_a := val [a]; val_b := val [b];
| h_Q := 0; h_R := diff[b]; h_P := (max(h_Q,h_R)+1)-diff[a];
| val [a] := val_b; val [b] := val_a;
| right [a] := right [b] {поддерево R}
| right [b] := left [b] {поддерево Q}
| left [b] := left [a] {поддерево P}
| left [a] := b;
| diff [b] := h_Q - h_P;
| diff [a] := h_R - (max (h_P, h_Q) + 1);
end;
procedure BR(a:integer);{большое правое вращение с корнем a}
| var b,c: 1..n; val_a,val_b,val_c: T;
| h_P,h_Q,h_R,h_S: integer;
begin
| b := right [a]; c := left [b]; {,c <> null}
| val_a := val [a]; val_b := val [b]; val_c := val [c];
| h_Q := 0; h_R := diff[c]; h_S := (max(h_Q,h_R)+1)+diff[b];
| h_P := 1 + max (h_S, h_S-diff[b]) - diff [a];
| val [a] := val_c; val [c] := val_a;
| left [b] := right [c] {поддерево R}
| right [c] := left [c] {поддерево Q}
| left [c] := left [a] {поддерево P}
| left [a] := c;
| diff [b] := h_S - h_R;
| diff [c] := h_Q - h_P;
| diff [a] := max (h_S, h_R) - max (h_P, h_Q);
end;
Левые вращения (большое и малое) записываются симметрично.
Процедуры добавления и удаления элементов пишутся как раньше, но только добавление и удаление должно сопровождаться коррекцией массива diff и восстановлением сбалансированности.
При этом используется процедура с такими свойствами:
дано: левое и правое поддеревья вершины с номером a сбалансированы, в самой вершине разница высот не больше 2, в поддереве с корнем a массив diff заполнен правильно;надо: поддерево с корнем a сбалансировано и массив diff соответственно изменен, d -- изменение его высоты (равно 0 или -1); в остальной части все осталось как было -- в частности, значения diff
procedure balance (a: integer; var d: integer);
begin {-2 <= diff[a] <= 2}
| if diff [a] = 2 then begin
| | b := right [a];
| | if diff [b] = -1 then begin
| | | BR (a); d := -1;
| | end else if diff [b] = 0 then begin
| | | SR (a); d := 0;
| | end else begin {diff [b] = 1}
| | | SR (a); d := - 1;
| | end;
| end else if diff [a] = -2 then begin
| | b := left [a];
| | if diff [b] = 1 then begin
| | | BL (a); d := -1;
| | end else if diff [b] = 0 then begin
| | | SL (a); d := 0;
| | end else begin {diff [b] = -1}
| | | SL (a); d := - 1;
| | end;
| end else begin {-2 < diff [a] < 2, ничего делать не надо}
| | d := 0;
| end;
end;
Восстановление сбалансированности требует движения от
листьев к корню, поэтому будем хранить в стеке путь от корня к
рассматриваемой в данный момент вершине. Элементами стека будут
пары ![]() вершина, направление движения из нее
вершина, направление движения из нее![]() ,т.е. значения типа
,т.е. значения типа
record
| vert: 1..n; {вершина}
| direction : (l, r); {l - левое, r - правое}
end;
Программа добавления элемента t теперь выглядит так:
if root = null then begin
| get_free (root);
| left[root] := null; right[root] := null; diff[root] := 0;
| val[root] := t;
end else begin
| x := root; ..сделать стек пустым
| {инвариант: осталось добавить t к непустому поддереву с
| корнем в x; стек содержит путь к x}
| while ((t < val [x]) and (left [x] <> null)) or
| | ((t > val [x]) and (right [x] <> null)) do begin
| | if t < val [x] then begin
| | | ..добавить в стек пару <x, l>
| | | x := left [x];
| | end else begin {t > val [x]}
| | | ..добавить в стек пару <x, r>
| | | x := right [x];
| | end;
| end;
| if t <> val [x] then begin {t нет в дереве}
| | get_free (i); val [i] := t;
| | left [i] := null; right [i] := null; diff [i] := 0;
| | if t < val [x] then begin
| | | ..добавить в стек пару <x, l>
| | | left [x] := i;
| | end else begin {t > val [x]}
| | | ..добавить в стек пару <x, r>
| | | right [x] := i;
| | end;
| | d := 1;
| | {инвариант: стек содержит путь к изменившемуся
| | поддереву, высота которого увеличилась по
| | сравнению с высотой в исходном дереве
| | на d (=0 или 1); это поддерево сбалансировано;
| | значения diff для его вершин правильны; в
| | остальном дереве все осталось как было -
| | в частности,значения diff}
| | while (d <> 0) and ..стек непуст do begin {d = 1}
| | | ..взять из стека пару в <v, direct>
| | | if direct = l then begin
| | | | if diff [v] = 1 then begin
| | | | | c := 0;
| | | | end else begin
| | | | | c := 1;
| | | | end;
| | | | diff [v] := diff [v] - 1;
| | | end else begin {direct = r}
| | | | if diff [v] = -1 then begin
| | | | | c := 0;
| | | | end else begin
| | | | | c := 1;
| | | | end;
| | | | diff [v] := diff [v] + 1;
| | | end;
| | | {c = изменение высоты поддерева с корнем в v по
| | | сравнению с исходным деревом; массив diff
| | | содержит правильные значения для этого поддерева;
| | | возможно нарушение сбалансированности в v}
| | | balance (v, d1); d := c + d1;
| | end;
| end;
end;
Легко проверить, что значение d может быть равно только
0 или 1 (но не -1): если c=0, то
diff[v]=0 и
балансировка не производится.
Программа удаления строится аналогично. Ее основной фрагмент таков:
{инвариант: стек содержит путь к изменившемуся поддереву,
высота которого изменилась по сравнению с высотой в
исходном дереве на d (=0 или -1); это поддерево
сбалансировано; значения diff для его вершин правильны;
в остальном дереве все осталось как было -
в частности, значения diff}
while (d <> 0) and ..стек непуст do begin
| {d = -1}
| ..взять из стека пару в <v, direct>
| if direct = l then begin
| | if diff [v] = -1 then begin
| | | c := -1;
| | end else begin
| | | c := 0;
| | end;
| | diff [v] := diff [v] + 1;
| end else begin {direct = r}
| | if diff [v] = 1 then begin
| | | c := -1;
| | end else begin
| | | c := 0;
| | end;
| | diff [v] := diff [v] - 1;
| end;
| {c = изменение высоты поддерева с корнем в v по срав-
| нению с исходным деревом; массив diff содержит
| правильные значения для этого поддерева;
| возможно нарушение сбалансированности в v}
| balance (v, d1);
| d := c + d1;
end;
Легко проверить, что значение d может быть равно только
0 или -1 (но не -2): если c=-1, то
diff[v]=0 и
балансировка не производится.
Отметим также, что наличие стека делает излишними
переменные father и direction (их роль теперь
играет вершина стека).![]()
![]() 12.2.6. Доказать, что при добавлении элемента
12.2.6. Доказать, что при добавлении элемента
(а) второй из трех случаев балансировки (см. рисунок на с. 12.2) невозможен;
(б) полная балансировка требует не более одного вращения
(после чего все дерево становится сбалансированным),
в то время как при удалении элемента может понадобиться
много вращений.![]()
Существуют и другие способы представления множеств,
гарантирующие число действий порядка ![]() на каждую операцию.
Опишем один из них (называемый Б-деревьями).
на каждую операцию.
Опишем один из них (называемый Б-деревьями).
До сих пор каждая вершина содержала один элемент хранимого
множества. Этот элемент служил границей между левым и правым
поддеревом. Будем теперь хранить в вершине ![]() элементов
множества (число k может меняться от вершины к вершине, а также
при добавлении и удалении новых элементов, см. далее). Эти k
элементов служат разделителями для k+1 поддерева. Пусть
фиксировано некоторое число
элементов
множества (число k может меняться от вершины к вершине, а также
при добавлении и удалении новых элементов, см. далее). Эти k
элементов служат разделителями для k+1 поддерева. Пусть
фиксировано некоторое число ![]() . Будем рассматривать деревья,
обладающие такими свойствами:
. Будем рассматривать деревья,
обладающие такими свойствами:
Добавление элемента происходит так. Если лист, в который он попадает, неполон (т.е. содержит менее 2t элементов), то нет проблем. Если он полон, то 2t+1 элемент (все элементы листа и новый элемент) разбиваем на два листа по t элементов и разделяющий их серединный элемент. Этот серединный элемент надо добавить в вершину предыдущего уровня. Это возможно, если в ней менее 2t элементов. Если и она полна, то ее разбивают на две, выделяют серединный элемент и т.д. Если в конце концов мы захотим добавить элемент в корень, а он окажется полным, то корень расщепляется на две вершины, а высота дерева увеличивается на 1 .
Удаление элемента, находящегося не в листе, сводится к удалению непосредственно следующего за ним, который находится в листе. Поэтому достаточно научиться удалять элемент из листа. Если лист при этом становится неполным, то его можно пополнить за счет соседнего листа -- если только и он не имеет минимально возможный размер t . Если же оба листа имеют размер t , то на них вместе 2t элементов, вместе с разделителем -- 2t+1 . После удаления одного элемента остается 2t элементов -- как раз на один лист. Если при этом вершина предыдущего уровня становится меньше нормы, процесс повторяется и т.д.
![]() 12.2.7. Реализовать описанную схему хранения множеств,
убедившись, что она также позволяет обойтись
12.2.7. Реализовать описанную схему хранения множеств,
убедившись, что она также позволяет обойтись ![]() действий
для операций включения, исключения и проверки принадлежности.
действий
для операций включения, исключения и проверки принадлежности.![]()
![]() 12.2.8. Можно определять сбалансированность дерева иначе:
требовать, чтобы для каждой вершины ее левое и правое поддеревья
имели не слишком сильно отличающиеся количества вершин.
(Преимущество такого определения состоит в том, что при
вращениях
не нарушается сбалансированность в вершинах, находящихся
ниже точки вращения.)
Реализовать на основе этой идеи способ хранения множеств,
гарантирующий оценку в
12.2.8. Можно определять сбалансированность дерева иначе:
требовать, чтобы для каждой вершины ее левое и правое поддеревья
имели не слишком сильно отличающиеся количества вершин.
(Преимущество такого определения состоит в том, что при
вращениях
не нарушается сбалансированность в вершинах, находящихся
ниже точки вращения.)
Реализовать на основе этой идеи способ хранения множеств,
гарантирующий оценку в ![]() действий для включения, удаления
и проверки принадлежности.
действий для включения, удаления
и проверки принадлежности.