 |
|
Поиск в строках, массивах, последовательностях:
Общие подпоследовательности, дистанция.
Укконен.
Метод вычисления расстояния между двумя строками и получения минимальной последовательности операций редактирования Укконена [Ukkonen, 1985] основан на подходе динамического программирования, однако требует O(dm) времени и памяти, где d – это расстояние между строками x и y, а m – меньшая из длин двух строк. Таким образом, этот метод эффективен, когда расстояния между строками малы, то есть когда строки похожи. Основная идея алгоритма состоит в нахождении самого дешевого пути в направленном графе в матрице di,j, в процессе чего избегаются ненужные вычисления di,j.
Как и ранее, будем считать, что m < n. Вспомним, что в методе динамического программирования di,j получают, выбирая минимальное из полученных с учетом предварительно вычисленных для соседей значений согласно формуле (11). По завершении вычисления dm,n, последовательность операций редактирования минимальной цены получают прослеживанием пути через матрицу, состоящего из переходов, дающих минимальные di,j.
Зависимости между элементами матрицы d можно представить направленными дугами – дуга из (i, j) в (i', j') существует только если di'j' получено из di,j. Полученный в результате граф зависимостей является подграфом графа, состоящего из всех узлов (i, j) и вертикальных, горизонтальных и диагональных (от верхнего левого к нижнему правому) дуг, соединяющих смежные узлы. Эти дуги означают, соответственно, удаления, вставки, а также замены и сопоставления. Поэтому с дугами можно сопоставить цены этих операций, и значение di,j будет, таким образом, задаваться суммой весов по любом пути из (0, 0) в (i, j). Взаимосвязь между дугами и ценами следующая.
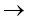 di,j w(xi,
di,j w(xi,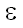 )
)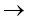 di,j w(
di,j w(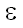 , yj)
, yj)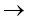 di,j w(xi,yj)
di,j w(xi,yj)Конечные значения на пути из (i,j) в (i', j') в графе зависимостей связаны следующим соотношением, где d – сумма цен всех дуг в пути:
| (45) |
Расстояние di,j между двумя строками является, таким образом, минимальной общей ценой пути из d0,0 в dm,n в графе зависимости.
Для определения самого дешевого пути в графе (Ахо, Хопкрофт и Ульман [Aho, Hopcroft, Ullman, 1974]) можно использовать алгоритм Дийкстры (Dijkstra), который сделает это за время O(mn log mn). Однако, топология графа позволяет найти и более эффективное решение, например, метод динамического программирования. Ниже будет показано, как можно сократить число входов массива d, которые нужно вычислить.
Значение dm,n вычисляется только по входам di,j на некотором пути из (0,0) в (m,n). Обратите внимание, что его вычисление требует времени O(n), так как любой такой путь содержит не больше m+n дуг. Рассмотрим задачу выяснения, превосходит ли dm,n некоторый порог, скажем, h. Из 11 можно видеть, что значения dij монотонно возрастают вдоль любого пути в графе зависимости. Таким образом, если dm,n < h, а некоторое di,j > h, то это di,j не может являться частью пути в (m, n).
Обозначим через wmin минимальную цену всех вставок и удалений, то есть
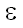 ), w( ), w(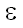 , a) : a , a) : a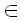 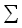 } } |
(46) |
для алфавита 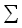 . Для ненулевых положительных весов wmin > 0. Кроме того, пронумеруем диагонали матрицы расстояний целыми числами k
. Для ненулевых положительных весов wmin > 0. Кроме того, пронумеруем диагонали матрицы расстояний целыми числами k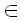 [-m, n] таким образом, чтобы диагональ k состояла из элементов (i, j), у которых j - i = k.
[-m, n] таким образом, чтобы диагональ k состояла из элементов (i, j), у которых j - i = k.
Рассмотрим произвольный путь из (i, j) в (i', j') в графе зависимости. Элемент (i, j) лежит на диагонали k = j - i, а (i', j') – на диагонали k' = j' - i'. Если k' - k < 0, то путь содержит не меньше |k' - k| удалений (вертикальных дуг), а если k' - k > 0, не меньше |k' - k| вставок (горизонтальных дуг). Из (45) мы имеем следующее:
| (47) |
Таким образом, di,j > |j - i|*wmin для каждого (i, j) на пути из (0,0) в (m, n). Кроме того, так как di,j < dm,n для любого (i, j) в пути, мы имеем следующее:
| (48) |
Для вычисления dm,n достаточно рассмотреть элементы на диагональной ленте dm,n/wmin < j - i < dm,n/wmin. На самом деле, эту ленту можно сузить еще больше, что и будет показано ниже.
Рассмотрим путь из (0, 0) в (m, n) в графе зависимости. Его можно разложить на два пути: из (0, 0) в (i, j) и из (i, j) в (m, n). Из (47) мы имеем следующее:
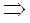 dm,n > (|j - i| + |(n - m) - (j - i)| * wmin dm,n > (|j - i| + |(n - m) - (j - i)| * wmin |
(49) |
Рассмотрим два случая: первый, когда j < i, а второй, когда j > i. В первом случае (49) принимает вид
 dm,n/wmin - (n - m) > -2(j - i) dm,n/wmin - (n - m) > -2(j - i) |
(50) |
С учетом того, что j - i целое число!!!!!!!!!!!!!!!!Ј 0, отсюда вытекает
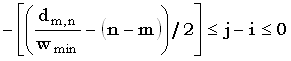 |
(51) |
Для случая, когда j > i, рассмотрим две возможности, а именно, n - m > j - i, и n - m < j - i. В первом случае (49) принимает вид
 dm,n/wmin > n - m dm,n/wmin > n - m |
(52) |
а во втором
 dm,n/wmin - (n - m) > 2(j - i) - 2(n - m) dm,n/wmin - (n - m) > 2(j - i) - 2(n - m) |
(53) |
С учетом того факта, что в данном случае j - i является целым числом > 0, получаем
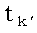 |
(54) |
Объединяя (51) и (54), получаем следующие ограничения на j - i для точек (i, j), лежащих на некотором пути из (0,0) в (m, n) в графе зависимости:
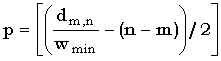 |
(55) |
Следствием из (55) является то, что для проверки выполнения неравенства d(x, y) < h можно ограничиться вычислением di,j, лежащих на ленте между диагоналями -p и n-m+p, где p = [(h/wmin - (n - m))/2].
Алгоритм для реализации этого порогового критерия приведен на рисунке (19). Проверка возвращает отрицательное значение, если критерий не выполнился, и значение dm,n, если оно меньше или равно пороговому. Критерий не выполняется в тривиальном случае, задаваемом выражением (52), так как расстояние должно быть по меньшей мере равно разности длин строк умножить на минимальную стоимость вставок и удалений. В не тривиальном случае вычисляются значения di,j на диагональной ленте, задаваемой (55). По завершении этих вычислений окончательное значение dm,n сравнивается с пороговым.
Рисунок 19: Пороговый критерий расстояния между строк Укконенаdistance_test(h) if h/wmin < N - M - ТРИВИАЛЬНЫЙ СЛУЧАЙ RETURN(-1) else - ИНИЦИАЛИЗАЦИЯ P = INT((H/Wmin - (n - m))/2) d0,0 = 0 for j = 1 to min{n, n - m + p} d0,j = d0,j-1 + w( , yj) - вычислить dm,n for i = 1 to m for j = max{0, i - p} to min{n, i + n - m + p} if j = 0 di,0 = di-1,0 + w(xi,
) else di,j = min{di-1,j + w(xi,*), di,j-1 + w(
,yj), di-1,j-1 + w(xi,yj)} if dm,n > h return(dm,n) else return(-1)
Рисунок 20: Вычисление расстояния между строками Укконенаh = (n - m + 1)wmin while (d = distance_test(h)) < 0 H = 2H
Для каждой из m+1 строк количество вычисляемых элементов матрицы не превосходит n-m+2p+1, что является O(h), как показано ниже.
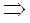 2p < h/wmin - (n - m) 2p < h/wmin - (n - m)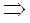 n - m + 2p + 1 < 1 + h/wmin= O(h) n - m + 2p + 1 < 1 + h/wmin= O(h) |
(56) |
Таким образом, пороговый критерий выполняется за время O(hm), и требует O(hm) памяти, если сохраняются только значения на диагональной ленте. Обратите внимание, что если требуется только значение расстояния между строками, то требования к памяти можно сократить до O(h) ячеек, так как для вычисления текущей строки требуются только значения предыдущей строки (алгоритм Хиршберга с линейным временем).
Чтобы найти фактическое расстояние между двумя строками, можно вызывать процедуру порогового критерия с последовательно возрастающими значениями h, пока критерий не выполнится. Алгоритм для этого приведен на рисунке 20. В начале порогу присваивается минимальное из возможных значений расстояния плюс wmin, которое затем последовательно удваивается. По завершении d равняется расстоянию между двумя строками.
Обозначим начальное пороговое значение h0, следующее, равное 2h0, h1, следующее, равное 22h0, h2, и т.д. Таким образом, r-е значение hr равно 2rh0. Если для определения d(x, y) требуется r вызовов distance_test, то всего требуется время 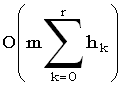 , то есть O(m(2hr - 1)), что равно O(mhr). Однако, так как d > hr/2, общая временная сложность равна O(dm). Фактическая последовательность редактирования может быть вычислена по завершению как в методе Вагнера-Фишера.
, то есть O(m(2hr - 1)), что равно O(mhr). Однако, так как d > hr/2, общая временная сложность равна O(dm). Фактическая последовательность редактирования может быть вычислена по завершению как в методе Вагнера-Фишера.
Укконен рассмотрел также частный случай, когда цены всех операций редактирования равны (то есть вычисление расстояния Левенштейна), для которого можно сократить требования к памяти и применить более эффективный, со временем O(dm), прямой метод вычисления d(x, y).
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.