[an error occurred while processing this directive]
We previously discussed the Discrete Log problem in the multiplicative group 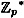 , where p is prime. This group is a cyclic group of order p - 1, and hence it is isomorphic to the additive group , where p is prime. This group is a cyclic group of order p - 1, and hence it is isomorphic to the additive group 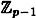 . By the discussion above, we know how to compute discrete logs efficiently in this additive group. This suggests that we could solve the Discrete Log problem in . By the discussion above, we know how to compute discrete logs efficiently in this additive group. This suggests that we could solve the Discrete Log problem in 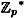 by “reducing” the problem to the the easily solved formulation in by “reducing” the problem to the the easily solved formulation in 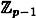 . .
Let us think about how this could be done. The statement that 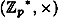 is isomorphic to is isomorphic to 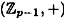 means that there is a bijection means that there is a bijection
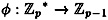
such that
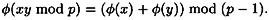
It follows easily that
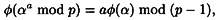
so we have that
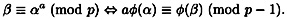
Hence, solving for a as described above, we have that
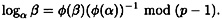
Consequently, if we have an efficient method of computing the isomorphism φ, then we would have an efficient algorithm to compute discrete logs in  . The catch is that there is no known general method to efficiently compute the isomorphism φ for an arbitrary prime p. Even though we know the two groups in question are isomorphic, we do not know an efficient algorithm to explicitly describe the isomorphism. . The catch is that there is no known general method to efficiently compute the isomorphism φ for an arbitrary prime p. Even though we know the two groups in question are isomorphic, we do not know an efficient algorithm to explicitly describe the isomorphism.
This method can be applied to the Discrete Log problem in any group G. If there is an efficient method of computing the isomorphism between H and 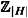 , then the discrete log problem in G described above can be solved efficiently. Conversely, it is not hard to see that an efficient method of computing discrete logs yields an efficient algorithm to compute the isomorphism between the two groups. , then the discrete log problem in G described above can be solved efficiently. Conversely, it is not hard to see that an efficient method of computing discrete logs yields an efficient algorithm to compute the isomorphism between the two groups.
This discussion has shown that the Discrete Log problem may be easy or (apparently) difficult, depending on the representation of the (cyclic) group that is used. So it may be useful to look at other groups in the hope of finding other settings where the Discrete Log problem seems to be intractible.
Two such classes of groups are
- 1. the multiplicative group of the Galois field GF(pn)
- 2. the group of an elliptic curve defined over a finite field.
We will discuss these two classes of groups in the next subsections.
5.2.1 Galois Fields
We have already discussed the fact that 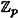 is a field if p is prime. However, there are other examples of finite fields not of this form. In fact, there is a finite field with q elements if q = pn where p is prime and n ≥ 1 is an integer. We will now describe very briefly how to construct such a field. First, we need several definitions. is a field if p is prime. However, there are other examples of finite fields not of this form. In fact, there is a finite field with q elements if q = pn where p is prime and n ≥ 1 is an integer. We will now describe very briefly how to construct such a field. First, we need several definitions.
DEFINITION 5.1 Suppose p is prime. Define 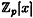 to be the set of all polynomials in the indeterminate x. By defining addition and multiplication of polynomials in the usual way (and reducing coefficients modulo p), we construct a ring. to be the set of all polynomials in the indeterminate x. By defining addition and multiplication of polynomials in the usual way (and reducing coefficients modulo p), we construct a ring.
For 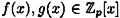 , we say that f(x) divides g(x) (notation: f(x) | g(x)) if there exists , we say that f(x) divides g(x) (notation: f(x) | g(x)) if there exists 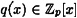 such that such that
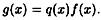
For 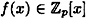 , define deg(f), the degree of f, to be the highest exponent in a term of f. , define deg(f), the degree of f, to be the highest exponent in a term of f.
Suppose f(x), g(x), 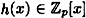 , and deg(f) = n ≥ 1. We define , and deg(f) = n ≥ 1. We define
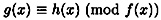
if
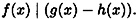
Notice the resemblance of the definition of congruence of polynomials to that of congruence of integers.
We are now going to define a ring of polynomials “modulo f(x)” which we denote by 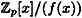 . The construction of . The construction of 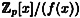 from from 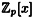 is based on the idea of congruences modulo f(x) and is analogous to the construction of is based on the idea of congruences modulo f(x) and is analogous to the construction of 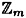 from from 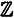 . .
Suppose deg(f) = n. If we divide g(x) by f(x), we obtain a (unique) quotient q(x) and remainder r(x), where
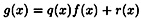
and
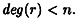
This can be done by usual long division of polynomials. Hence any polynomial in 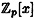 is congruent modulo f(x) to a unique polynomial of degree at most n - 1. is congruent modulo f(x) to a unique polynomial of degree at most n - 1.
Now we define the elements of 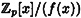 to be the pn polynomials in to be the pn polynomials in 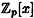 of degree at most n - 1. Addition and multiplication in of degree at most n - 1. Addition and multiplication in 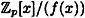 is defined as in is defined as in 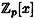 , followed by a reduction modulo f(x). Equipped with these operations, , followed by a reduction modulo f(x). Equipped with these operations, 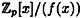 is a ring. is a ring.
Recall that  is a field if and only if m is prime, and multiplicative inverses can be found using the Euclidean algorithm. A similar situation holds for is a field if and only if m is prime, and multiplicative inverses can be found using the Euclidean algorithm. A similar situation holds for 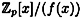 . The analog of primality for polynomials is irreducibility, which we define as follows: . The analog of primality for polynomials is irreducibility, which we define as follows:
DEFINITION 5.2 A polynomial 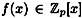 is said to be irreducible if there do not exist polynomials is said to be irreducible if there do not exist polynomials 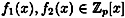 such that such that
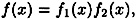
where deg(f1) > 0 and deg (f2) > 0.
A very important fact is that 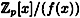 is a field if and only if f(x) is irreducible. Further, multiplicative inverses in is a field if and only if f(x) is irreducible. Further, multiplicative inverses in 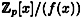 can be computed using a straightforward modification of the (extended) Euclidean algorithm. can be computed using a straightforward modification of the (extended) Euclidean algorithm.
Here is an example to illustrate the concepts described above.
Example 5.6
Let’s attempt to construct a field having eight elements. This can be done by finding an irreducible polynomial of degree three in 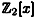 . It is sufficient to consider the polynomials having constant term equal to 1, since any polynomial with constant term 0 is divisible by x and hence is reducible. There are four such polynomials: . It is sufficient to consider the polynomials having constant term equal to 1, since any polynomial with constant term 0 is divisible by x and hence is reducible. There are four such polynomials:
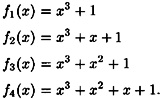
Now, f1 (x) is reducible, since
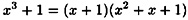
(remember that all coefficients are to be reduced modulo 2). Also, f4 is reducible since
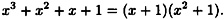
However, f2(x) and f3(x) are both irreducible, and either one can be used to construct a field having eight elements.
Let us use f2(x), and thus construct the field 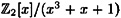 . The eight field elements are the eight polynomials 0, 1, x, x + 1, x2, x2 + 1, x2 + x and x2 + x + 1. . The eight field elements are the eight polynomials 0, 1, x, x + 1, x2, x2 + 1, x2 + x and x2 + x + 1.
To compute a product of two field elements, we multiple the two polynomials together, and reduce modulo x3 + x + 1 (i.e., divide by x3 + x + 1 and find the remainder polynomial). Since we are dividing by a polynomial of degree three, the remainder will have degree at most two and hence is an element of the field.

|






















