Intent

Given a language, define a represention for its grammar along with an interpreter that uses the representation to interpret sentences in the language.

Motivation

If a particular kind of problem occurs often enough, then it might be worthwhile to express instances of the problem as sentences in a simple language. Then you can build an interpreter that solves the problem by interpreting these sentences.

For example, searching for strings that match a pattern is a common problem. Regular expressions are a standard language for specifying patterns of strings. Rather than building custom algorithms to match each pattern against strings, search algorithms could interpret a regular expression that specifies a set of strings to match.

The Interpreter pattern describes how to define a grammar for simple languages, represent sentences in the language, and interpret these sentences. In this example, the pattern describes how to define a grammar for regular expressions, represent a particular regular expression, and how to interpret that regular expression.

Suppose the following grammar defines the regular expressions:

    expression ::= literal | alternation | sequence | repetition |
                   '(' expression ')'
    alternation ::= expression  '|' expression
    sequence ::= expression '&' expression
    repetition ::= expression '*'
    literal ::= 'a' | 'b' | 'c' | ... { 'a' | 'b' | 'c' | ... }*

The symbol expression is the start symbol, and literal is a terminal symbol defining simple words.

The Interpreter pattern uses a class to represent each grammar rule. Symbols on the right-hand side of the rule are instance variables of these classes. The grammar above is represented by five classes: an abstract class RegularExpression and its four subclasses LiteralExpression, AlternationExpression, SequenceExpression, and RepetitionExpression. The last three classes define variables that hold subexpressions.

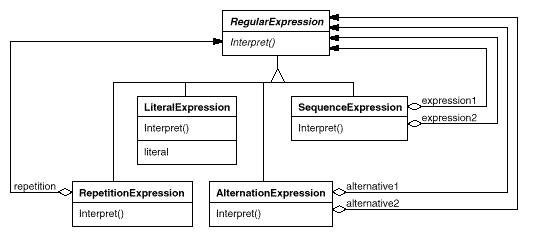
Every regular expression defined by this grammar is represented by an abstract syntax tree made up of instances of these classes. For example, the abstract syntax tree

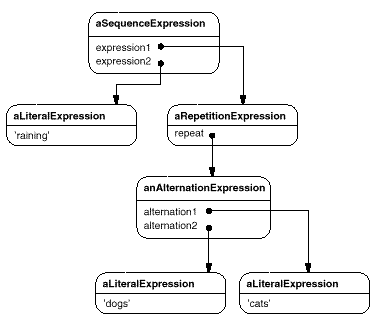
represents the regular expression

    raining & (dogs | cats) *

We can create an interpreter for these regular expressions by defining the Interpret operation on each subclass of RegularExpression. Interpret takes as an argument the context in which to interpret the expression. The context contains the input string and information on how much of it has been matched so far. Each subclass of RegularExpression implements Interpret to match the next part of the input string based on the current context. For example,

• LiteralExpression will check if the input matches the literal it defines,
• AlternationExpression will check if the input matches any of its alternatives,
• RepetitionExpression will check if the input has multiple copies of expression it repeats,

and so on.

Applicability

Use the Interpreter pattern when there is a language to interpret, and you can represent statements in the language as abstract syntax trees. The Interpreter pattern works best when

• the grammar is simple. For complex grammars, the class hierarchy for the grammar becomes large and unmanageable. Tools such as parser generators are a better alternative in such cases. They can interpret expressions without building abstract syntax trees, which can save space and possibly time.
• efficiency is not a critical concern. The most efficient interpreters are usually not implemented by interpreting parse trees directly but by first translating them into another form. For example, regular expressions are often transformed into state machines. But even then, the translator can be implemented by the Interpreter pattern, so the pattern is still applicable.

Structure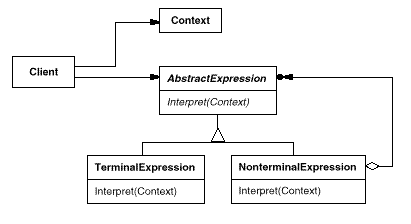

Participants

• AbstractExpression (RegularExpression)
• declares an abstract Interpret operation that is common to all nodes in the abstract syntax tree.
• TerminalExpression (LiteralExpression)
• implements an Interpret operation associated with terminal symbols in the grammar.
• an instance is required for every terminal symbol in a sentence.
• NonterminalExpression (AlternationExpression, RepetitionExpression, SequenceExpressions)
• one such class is required for every rule R ::= R₁ R₂ ... R_n in the grammar.
• maintains instance variables of type AbstractExpression for each of the symbols R₁ through R_n.
• implements an Interpret operation for nonterminal symbols in the grammar. Interpret typically calls itself recursively on the variables representing R₁ through R_n.
• Context
• contains information that's global to the interpreter.
• Client
• builds (or is given) an abstract syntax tree representing a particular sentence in the language that the grammar defines. The abstract syntax tree is assembled from instances of the NonterminalExpression and TerminalExpression classes.
• invokes the Interpret operation.

Collaborations

• The client builds (or is given) the sentence as an abstract syntax tree of NonterminalExpression and TerminalExpression instances. Then the client initializes the context and invokes the Interpret operation.
• Each NonterminalExpression node defines Interpret in terms of Interpret on each subexpression. The Interpret operation of each TerminalExpression defines the base case in the recursion.
• The Interpret operations at each node use the context to store and access the state of the interpreter.

Consequences

The Interpreter pattern has the following benefits and liabilities:

1. It's easy to change and extend the grammar. Because the pattern uses classes to represent grammar rules, you can use inheritance to change or extend the grammar. Existing expressions can be modified incrementally, and new expressions can be defined as variations on old ones.
2. Implementing the grammar is easy, too. Classes defining nodes in the abstract syntax tree have similar implementations. These classes are easy to write, and often their generation can be automated with a compiler or parser generator.
3. Complex grammars are hard to maintain. The Interpreter pattern defines at least one class for every rule in the grammar (grammar rules defined using BNF may require multiple classes). Hence grammars containing many rules can be hard to manage and maintain. Other design patterns can be applied to mitigate the problem (see Implementation). But when the grammar is very complex, other techniques such as parser or compiler generators are more appropriate.
4. Adding new ways to interpret expressions. The Interpreter pattern makes it easier to evaluate an expression in a new way. For example, you can support pretty printing or type-checking an expression by defining a new operation on the expression classes. If you keep creating new ways of interpreting an expression, then consider using the Visitor (331) pattern to avoid changing the grammar classes.

Implementation

The Interpreter and Composite (163) patterns share many implementation issues. The following issues are specific to Interpreter:

1. Creating the abstract syntax tree. The Interpreter pattern doesn't explain how to create an abstract syntax tree. In other words, it doesn't address parsing. The abstract syntax tree can be created by a table-driven parser, by a hand-crafted (usually recursive descent) parser, or directly by the client.
2. Defining the Interpret operation. You don't have to define the Interpret operation in the expression classes. If it's common to create a new interpreter, then it's better to use the Visitor (331) pattern to put Interpret in a separate "visitor" object. For example, a grammar for a programming language will have many operations on abstract syntax trees, such as as type-checking, optimization, code generation, and so on. It will be more likely to use a visitor to avoid defining these operations on every grammar class.
3. Sharing terminal symbols with the Flyweight pattern. Grammars whose sentences contain many occurrences of a terminal symbol might benefit from sharing a single copy of that symbol. Grammars for computer programs are good examples—each program variable will appear in many places throughout the code. In the Motivation example, a sentence can have the terminal symbol dog (modeled by the LiteralExpression class) appearing many times.

   Terminal nodes generally don't store information about their position in the abstract syntax tree. Parent nodes pass them whatever context they need during interpretation. Hence there is a distinction between shared (intrinsic) state and passed-in (extrinsic) state, and the Flyweight (195) pattern applies.

   For example, each instance of LiteralExpression for dog receives a context containing the substring matched so far. And every such LiteralExpression does the same thing in its Interpret operation—it checks whether the next part of the input contains a dog---no matter where the instance appears in the tree.

Sample Code

Here are two examples. The first is a complete example in Smalltalk for checking whether a sequence matches a regular expression. The second is a C++ program for evaluating Boolean expressions.

The regular expression matcher tests whether a string is in the language defined by the regular expression. The regular expression is defined by the following grammar:

    expression ::= literal | alternation | sequence | repetition |
                   '(' expression ')'
    alternation ::= expression  '|' expression
    sequence ::= expression '&' expression
    repetition ::= expression 'repeat'
    literal ::= 'a' | 'b' | 'c' | ... { 'a' | 'b' | 'c' | ... }*

This grammar is a slight modification of the Motivation example. We changed the concrete syntax of regular expressions a little, because symbol "*" can't be a postfix operation in Smalltalk. So we use repeat instead. For example, the regular expression

    (('dog ' | 'cat ') repeat & 'weather')

matches the input string "dog dog cat weather".

To implement the matcher, we define the five classes described on page 243. The class SequenceExpression has instance variables expression1 and expression2 for its children in the abstract syntax tree. AlternationExpression stores its alternatives in the instance variables alternative1 and alternative2, while RepetitionExpression holds the expression it repeats in its repetition instance variable. LiteralExpression has a components instance variable that holds a list of objects (probably characters). These represent the literal string that must match the input sequence.

The match: operation implements an interpreter for the regular expression. Each of the classes defining the abstract syntax tree implements this operation. It takes inputState as an argument representing the current state of the matching process, having read part of the input string.

This current state is characterized by a set of input streams representing the set of inputs that the regular expression could have accepted so far. (This is roughly equivalent to recording all states that the equivalent finite state automata would be in, having recognized the input stream to this point).

The current state is most important to the repeat operation. For example, if the regular expression were

    'a' repeat

then the interpreter could match "a", "aa", "aaa", and so on. If it were

    'a' repeat & 'bc'

then it could match "abc", "aabc", "aaabc", and so on. But if the regular expression were

    'a' repeat & 'abc'

then matching the input "aabc" against the subexpression "'a' repeat" would yield two input streams, one having matched one character of the input, and the other having matched two characters. Only the stream that has accepted one character will match the remaining "abc".

Now we consider the definitions of match: for each class defining the regular expression. The definition for SequenceExpression matches each of its subexpressions in sequence. Usually it will eliminate input streams from its inputState.

    match: inputState
        ^ expression2 match: (expression1 match: inputState).

An AlternationExpression will return a state that consists of the union of states from either alternative. The definition of match: for AlternationExpression is

    match: inputState
        | finalState |
        finalState := alternative1 match: inputState.
        finalState addAll: (alternative2 match: inputState).
        ^ finalState

The match: operation for RepetitionExpression tries to find as many states that could match as possible:

    match: inputState
        | aState finalState |
        aState := inputState.
        finalState := inputState copy.
        [aState isEmpty]
            whileFalse:
                [aState := repetition match: aState.
                finalState addAll: aState].
            ^ finalState

Its output state usually contains more states than its input state, because a RepetitionExpression can match one, two, or many occurrences of repetition on the input state. The output states represent all these possibilities, allowing subsequent elements of the regular expression to decide which state is the correct one.

Finally, the definition of match: for LiteralExpression tries to match its components against each possible input stream. It keeps only those input streams that have a match:

    match: inputState
        | finalState tStream |
        finalState := Set new.
        inputState
            do:
                [:stream | tStream := stream copy.
                    (tStream nextAvailable:
                         components size
                    ) = components
                        ifTrue: [finalState add: tStream]
                ].
            ^ finalState

The nextAvailable: message advances the input stream. This is the only match: operation that advances the stream. Notice how the state that's returned contains a copy of the input stream, thereby ensuring that matching a literal never changes the input stream. This is important because each alternative of an AlternationExpression should see identical copies of the input stream.

Now that we've defined the classes that make up an abstract syntax tree, we can describe how to build it. Rather than write a parser for regular expressions, we'll define some operations on the RegularExpression classes so that evaluating a Smalltalk expression will produce an abstract syntax tree for the corresponding regular expression. That lets us use the built-in Smalltalk compiler as if it were a parser for regular expressions.

To build the abstract syntax tree, we'll need to define "|", "repeat", and "&" as operations on RegularExpression. These operations are defined in class RegularExpression like this:

    & aNode
        ^ SequenceExpression new
            expression1: self expression2: aNode asRExp
    
    repeat
        ^ RepetitionExpression new repetition: self
    
    | aNode
        ^ AlternationExpression new
        alternative1: self alternative2: aNode asRExp
    
    asRExp 
        ^ self

The asRExp operation will convert literals into RegularExpressions. These operations are defined in class String:

    & aNode
        ^ SequenceExpression new
            expression1: self asRExp expression2: aNode asRExp
    
    repeat
        ^ RepetitionExpression new repetition: self
    
    | aNode
        ^ AlternationExpression new
            alternative1: self asRExp alternative2: aNode asRExp
    
    asRExp
        ^ LiteralExpression new components: self

If we defined these operations higher up in the class hierarchy (SequenceableCollection in Smalltalk-80, IndexedCollection in Smalltalk/V), then they would also be defined for classes such as Array and OrderedCollection. This would let regular expressions match sequences of any kind of object.

The second example is a system for manipulating and evaluating Boolean expressions implemented in C++. The terminal symbols in this language are Boolean variables, that is, the constants true and false. Nonterminal symbols represent expressions containing the operators and, or, and not. The grammar is defined as follows¹:

    BooleanExp ::= VariableExp | Constant | OrExp | AndExp | NotExp |
                   '(' BooleanExp ')'
    AndExp ::= BooleanExp  'and' BooleanExp
    OrExp ::= BooleanExp  'or' BooleanExp
    NotExp ::= 'not' BooleanExp
    Constant ::= 'true' |  'false'
    VariableExp ::= 'A' | 'B' | ... | 'X' | 'Y' | 'Z'

We define two operations on Boolean expressions. The first, Evaluate, evaluates a Boolean expression in a context that assigns a true or false value to each variable. The second operation, Replace, produces a new Boolean expression by replacing a variable with an expression. Replace shows how the Interpreter pattern can be used for more than just evaluating expressions. In this case, it manipulates the expression itself.

We give details of just the BooleanExp, VariableExp, and AndExp classes here. Classes OrExp and NotExp are similar to AndExp. The Constant class represents the Boolean constants.

BooleanExp defines the interface for all classes that define a Boolean expression:

    class BooleanExp {
    public:
        BooleanExp();
        virtual ~BooleanExp();
    
        virtual bool Evaluate(Context&) = 0;
        virtual BooleanExp* Replace(const char*, BooleanExp&) = 0;
        virtual BooleanExp* Copy() const = 0;
    };

The class Context defines a mapping from variables to Boolean values, which we represent with the C++ constants true and false. Context has the following interface:

    class Context {
    public:
        bool Lookup(const char*) const;
        void Assign(VariableExp*, bool);
    };

A VariableExp represents a named variable:

    class VariableExp : public BooleanExp {
    public:
        VariableExp(const char*);
        virtual ~VariableExp();
    
        virtual bool Evaluate(Context&);
        virtual BooleanExp* Replace(const char*, BooleanExp&);
        virtual BooleanExp* Copy() const;
    private:
        char* _name;
    };

The constructor takes the variable's name as an argument:

    VariableExp::VariableExp (const char* name) {
        _name = strdup(name);
    }

Evaluating a variable returns its value in the current context.

    bool VariableExp::Evaluate (Context& aContext) {
        return aContext.Lookup(_name);
    }

Copying a variable returns a new VariableExp:

    BooleanExp* VariableExp::Copy () const {
        return new VariableExp(_name);
    }

To replace a variable with an expression, we check to see if the variable has the same name as the one it is passed as an argument:

    BooleanExp* VariableExp::Replace (
        const char* name, BooleanExp& exp
    ) {
        if (strcmp(name, _name) == 0) {
            return exp.Copy();
        } else {
            return new VariableExp(_name);
       }
    }

An AndExp represents an expression made by ANDing two Boolean expressions together.

    class AndExp : public BooleanExp {
    public:
        AndExp(BooleanExp*, BooleanExp*);
        virtual ~ AndExp();
    
        virtual bool Evaluate(Context&);
        virtual BooleanExp* Replace(const char*, BooleanExp&);
        virtual BooleanExp* Copy() const;
    private:
        BooleanExp* _operand1;
        BooleanExp* _operand2;
    };
    
    AndExp::AndExp (BooleanExp* op1, BooleanExp* op2) {
        _operand1 = op1;
        _operand2 = op2;
    }

Evaluating an AndExp evaluates its operands and returns the logical "and" of the results.

    bool AndExp::Evaluate (Context& aContext) {
        return
            _operand1->Evaluate(aContext) &&
            _operand2->Evaluate(aContext);
    }

An AndExp implements Copy and Replace by making recursive calls on its operands:

    BooleanExp* AndExp::Copy () const {
        return
            new AndExp(_operand1->Copy(), _operand2->Copy());
    }
    
    BooleanExp* AndExp::Replace (const char* name, BooleanExp& exp) {
        return
            new AndExp(
                _operand1->Replace(name, exp),
                _operand2->Replace(name, exp)
            );
    }

Now we can define the Boolean expression

    (true and x) or (y and (not x))

and evaluate it for a given assignment of true or false to the variables x and y:

    BooleanExp* expression;
    Context context;
    
    VariableExp* x = new VariableExp("X");
    VariableExp* y = new VariableExp("Y");
    
    expression = new OrExp(
        new AndExp(new Constant(true), x),
        new AndExp(y, new NotExp(x))
    );
    
    context.Assign(x, false);
    context.Assign(y, true);
    
    bool result = expression->Evaluate(context);

The expression evaluates to true for this assignment to x and y. We can evaluate the expression with a different assignment to the variables simply by changing the context.

Finally, we can replace the variable y with a new expression and then reevaluate it:

    VariableExp* z = new VariableExp("Z");
    NotExp not_z(z);
    
    BooleanExp* replacement = expression->Replace("Y", not_z);
    
    context.Assign(z, true);
    
    result = replacement->Evaluate(context);

This example illustrates an important point about the Interpreter pattern: many kinds of operations can "interpret" a sentence. Of the three operations defined for BooleanExp, Evaluate fits our idea of what an interpreter should do most closely—that is, it interprets a program or expression and returns a simple result.

However, Replace can be viewed as an interpreter as well. It's an interpreter whose context is the name of the variable being replaced along with the expression that replaces it, and whose result is a new expression. Even Copy can be thought of as an interpreter with an empty context. It may seem a little strange to consider Replace and Copy to be interpreters, because these are just basic operations on trees. The examples in Visitor (331) illustrate how all three operations can be refactored into a separate "interpreter" visitor, thus showing that the similarity is deep.

The Interpreter pattern is more than just an operation distributed over a class hierarchy that uses the Composite (163) pattern. We consider Evaluate an interpreter because we think of the BooleanExp class hierarchy as representing a language. Given a similar class hierarchy for representing automotive part assemblies, it's unlikely we'd consider operations like Weight and Copy as interpreters even though they are distributed over a class hierarchy that uses the Composite pattern—we just don't think of automotive parts as a language. It's a matter of perspective; if we started publishing grammars of automotive parts, then we could consider operations on those parts to be ways of interpreting the language.

Known Uses

The Interpreter pattern is widely used in compilers implemented with object-oriented languages, as the Smalltalk compilers are. SPECTalk uses the pattern to interpret descriptions of input file formats [Sza92]. The QOCA constraint-solving toolkit uses it to evaluate constraints [HHMV92].

Considered in its most general form (i.e., an operation distributed over a class hierarchy based on the Composite pattern), nearly every use of the Composite pattern will also contain the Interpreter pattern. But the Interpreter pattern should be reserved for those cases in which you want to think of the class hierarchy as defining a language.

Related Patterns

Composite (163): The abstract syntax tree is an instance of the Composite pattern.

Flyweight (195) shows how to share terminal symbols within the abstract syntax tree.

Iterator (257): The interpreter can use an Iterator to traverse the structure.

Visitor (331) can be used to maintain the behavior in each node in the abstract syntax tree in one class.

Iterator
Command

¹For simplicity, we ignore operator precedence and assume it's the responsibility of whichever object constructs the syntax tree.