Быстрая сортировка
Хотя идея Шелла значительно улучшает сортировку вставками, резервы еще
остаются. Один из наиболее известных алгоритмов сортировки - быстрая сортировка,
предложенная Ч.Хоором. Метод и в самом деле очень быстр, недаром по-английски
его так и величают QuickSort к неудовольствию всех спелл-чекеров ("...Шишков
прости: не знаю, как перевести").
Этому методу требуется O(n lg n) в среднем
и O(n2) в худшем случае. К счастью, если
принять адекватные предосторожности, наихудший случай крайне маловероятен.
Быстрый поиск не является устойчивым. Кроме того, ему требуется стек, т.е.
он не является и методом сортировки на месте. Дальнейшую информацию можно
получить в работе Кормена
[1990].
Теория
Алгоритм разбивает сортируемый массив на разделы, затем рекурсивно сортирует
каждый раздел. В функции Partition (рис. 2.3) один из элементов массива
выбирается в качестве центрального. Ключи, меньшие центрального следует
расположить слева от него, те, которые больше, - справа.
int function Partition (Array A, int Lb, int Ub);
begin
select a pivot from A[Lb]...A[Ub];
reorder A[Lb]...A[Ub] such that:
all values to the left of the pivot are <= pivot
all values to the right of the pivot are >= pivot
return pivot position;
end;
procedure QuickSort (Array A, int Lb, int Ub);
begin
if Lb < Ub then
M = Partition (A, Lb, Ub);
QuickSort (A, Lb, M - 1);
QuickSort (A, M + 1, Ub);
end;
|
Рис. 2-3: Быстрый поиск
На рис. 2.4(a) в качестве центрального выбран элемент 3. Индексы начинают
изменяться с концов массива. Индекс i начинается слева и используется для
выбора элементов, которые больше центрального, индекс j начинается справа
и используется для выбора элементов, которые меньше центрального. Эти элементы
меняются местами - см. рис. 2.4(b). Процедура QuickSort рекурсивно
сортирует два подмассива, в результате получается массив, представленный
на рис. 2.4(c).
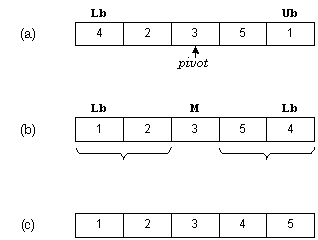
Рис 2-4: Пример работы алгоритма Quicksort
В процессе сортировки может потребоваться передвинуть центральный элемент.
Если нам повезет, выбранный элемент окажется медианой значений массива,
т.е. разделит его пополам. Предположим на минутку, что это и в самом деле
так. Поскольку на каждом шагу мы делим массив пополам, а функция Partition
в конце концов просмотрит все n элементов, время работы алгоритма есть
O(n lg n).
В качестве центрального функция Partition может попросту брать
первый элемент (A[Lb]). Все остальные элементы массива мы
сравниваем с центральным и передвигаем либо влево от него, либо вправо.
Есть, однако, один случай, который безжалостно разрушает эту прекрасную
простоту. Предположим, что наш массив с самого начала отсортирован. Функция
Partition всегда будет получать в качестве центрального минимальный
элемент и потому разделит массив наихудшим способом: в левом разделе окажется
один элемент, соответственно, в правом останется Ub - Lb
элементов. Таким образом, каждый рекурсивный вызов процедуры quicksort
всего лишь уменьшит длину сортируемого массива на 1. В результате для выполнения
сортировки понадобится n рекурсивных вызовов, что приводит к времени работы
алгоритма порядка O(n2). Один из способов
побороть эту проблему - случайно выбирать центральный элемент. Это сделает
наихудший случай чрезвычайно маловероятным.
Реализация
В приведенной реализации алгоритма на Си операторы
typedef T и compGT следует изменить так, чтобы они соответствовали
данным, хранимым в массиве. По сравнению с основным алгоритмом имеются
некоторые улучшения:
-
В качестве центрального в функции partition выбирается элемент,
расположенный в середине. Такой выбор улучшает оценку среднего времени
работы, если массив упорядочен лишь частично. Наихудшая для этой реализации
ситуация возникает в случае, когда каждый раз при работе partition
в качестве центрального выбирается максимальный или минимальный элемент.
-
Для коротких массивов вызывается insertSort. Из-за рекурсии и других
"накладных расходов" быстрый поиск оказывается не столь уж быстрым для
коротких массивов. Поэтому, если в массиве меньше 12 элементов, вызывается
сортировка вставками. Пороговое значение не критично - оно сильно зависит
от качества генерируемого кода.
-
Если последний оператор функции является вызовом этой функции, говорят
о хвостовой рекурсии. Ее имеет смысл заменять на итерации - в этом случае
лучше используется стек. Это сделано при втором вызове QuickSort
на рис. 2.3.
-
После разбиения сначала сортируется меньший раздел. Это также приводит
к лучшему использованию стека, поскольку короткие разделы сортируются быстрее
и им нужен более короткий стек.
Функция qsort из стандартной библиотеки
Си основана на алгоритме quicksort. Для этой реализации рекурсия была заменена
на итерации. В таблице 2.1 приводится время и размер стека, затрачиваемые
до и после описанных улучшений.
кол-во
элементов |
время (µs) |
размер стека |
| до |
после |
до |
после |
| 16 |
103 |
51 |
540 |
28 |
| 256 |
1,630 |
911 |
912 |
112 |
| 4,096 |
34,183 |
20,016 |
1,908 |
168 |
| 65,536 |
658,003 |
460,737 |
2,436 |
252 |
Таблица 2.1: Влияние улучшений на скорость работы и размер стека
