LR-процессы

Два отличия LR(1)-разбора от LL(1)-разбора: во-первых, строится не левый вывод, а правый, во-вторых, он строится не с   начала, а с конца. (Вывод в КС-грамматике называется правым, если на каждом шаге замене подвергается самый правый нетерминал.)


$\scriptstyle{\blacktriangleright}$ 14.1.1. Доказать, что если слово, состоящее из терминалов, выводимо, то оно имеет правый вывод.$\scriptstyle\blacktriangleleft$

Нам будет удобно смотреть на правый вывод << задом наперед>>. Определим понятие LR-процесса над словом  A . В этом процессе, помимо A , будет участвовать и другое слово S , которое может содержать как терминалы, так и нетерминалы. Вначале слово S пусто. В ходе LR-процесса разрешены два вида действий:

(1)
можно перенести первый символ слова A (его называют очередным символом и обозначают Next) в конец слова S , удалив его из A (это действие называют сдвигом); 
(2)
если правая часть одного из правил грамматики оказалась концом слова S , то разрешается заменить ее на нетерминал, стоящий в левой части этого правила; при этом слово A не меняется. (Это действие называют сверткой, или приведением.  

Отметим, что LR-процесс не является детерминированным: в одной и той же ситуации могут быть разрешены разные действия.

Говорят, что LR-процесс на слове A успешно завершается, если слово A становится пустым, а в слове S остается единственный нетерминал -- начальный нетерминал грамматики.


$\scriptstyle{\blacktriangleright}$ 14.1.2. Доказать, что для любого слова A (из терминалов) успешно завершающийся LR-процесс существует тогда и только тогда, когда слово A выводимо в грамматике. В ходе доказательства установить взаимно однозначное соответствие между правыми выводами и успешно завершающимися LR-процессами.

Решение. При сдвиге слово SA не меняется, при свертке слово SA подвергается преобразованию, обратному шагу вывода. Этот вывод будет правым, так как сворачивается конец S , а в A все символы -- терминальные. Таким образом, каждому LR-процессу соответствует правый вывод. Обратное соответствие: пусть дан правый вывод. Представим себе, что за последним нетерминалом в слове стоит перегородка. Применив к этому нетерминалу правило грамматики, мы должны сдвинуть перегородку влево (если правая часть правила кончается на терминал). Разбивая этот сдвиг на отдельные шаги, получим процесс, в точности обратный LR-процессу.

Поскольку в ходе LR-процесса все изменения в слове S происходят с правого конца, слово S называют стеком LR-процесса.

Задача построения правого вывода для данного слова сводится, таким образом, к правильному выбору очередного шага LR-процесса. Нам нужно решить, будем ли мы делать сдвиг или свертку, и если свертку, то по какому правилу -- ведь подходящих правил может быть несколько. В LR(1)-алгоритме это решение принимается на основе S и первого символа слова A ; если используется только S , то говорят о LR(0)-алгоритме. (Точные определения смотри ниже.)

Пусть фиксирована грамматика, в которой из любого нетерминала можно вывести какое-либо слово из терминалов. (Это ограничение мы будет всегда предполагать выполненным.)

Пусть ${\hbox{\tt K}}\to{\hbox{\tt U}}$ -- одно из правил грамматики (K -- нетерминал, U -- слово из терминалов и нетерминалов). Определим множество слов (из терминалов и нетерминалов), называемое левым контекстом правила ${\hbox{\tt K}}\to{\hbox{\tt U}}$.    (Обозначение: ${\hbox{\rm ЛевКонт}}({\hbox{\tt K}}\to{\hbox{\tt U}})$.) По определению в него входят все слова, которые являются содержимым стека непосредственно перед сверткой U в K в ходе некоторого успешно завершающегося LR-процесса.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.3. Переформулировать это определение на языке правых выводов.

Решение. Рассмотрим все правые выводы вида \begin{displaymath} \langle{\hbox{\rm начальный нетерминал}}\rangle \leadsto{\hbox{\tt XKA}} \to {\hbox{\tt XUA}},\end{displaymath}где A -- слово из терминалов, X -- слово из терминалов и нетерминалов. Все возникающие при этом слова XU и образуют левый контекст правила ${\hbox{\tt K}}\to{\hbox{\tt U}}$. Чтобы убедиться в этом, следует вспомнить, что мы предполагаем, что из любого нетерминала можно вывести какое-то слово из терминалов, так что правый вывод слова XUA может быть продолжен до правого вывода какого-то слова из терминалов.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.4. Все слова из ${\hbox{\rm ЛевКонт}}({\hbox{\tt K}}\to{\hbox{\tt U}})$ кончаются, очевидно, на U. Доказать, что если у всех них этот конец U отбросить, то полученное множество слов не зависит от того, какое из правил для нетерминала K выбрано. (Это множество обозначается ${\hbox{\rm Лев}}({\hbox{\tt K}})$.)

 

Решение. Из предыдущей задачи ясно, что ${\hbox{\rm Лев}}({\hbox{\tt K}})$-- это все, что может появиться в правых выводах левее самого правого нетерминала K.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.5. Доказать, что в предыдущей фразе можно отбросить слова << самого правого>>: ${\hbox{\rm Лев}}({\hbox{\tt K}})$ -- это все то, что может появляться в правых выводах левее любого вхождения нетерминала K.

Решение. Продолжив построение правого вывода, все нетерминалы справа от K можно заменить на терминалы (а слева от K при этом ничего не изменится).$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.6. Построить грамматику, содержащую для каждого нетерминала K исходной грамматики нетерминал $\langle{\hbox{\rm Лев}}{\hbox{\tt K}}\rangle$,причем следующее свойство должно выполняться для любого нетерминала K исходной грамматики: в новой грамматике из $\langle{\hbox{\rm Лев}}{\hbox{\tt K}}\rangle$выводимы все элементы ${\hbox{\rm Лев}}({\hbox{\tt K}})$ и только они.

Решение. Пусть P -- начальный нетерминал грамматики. Тогда в новой грамматике будет правило \begin{displaymath} \langle{\hbox{\rm Лев}}{\hbox{\tt P}}\rangle \to \qquad\qquad(\hbox{пустое слово})\end{displaymath}Для каждого правила исходной грамматики, например, правила \begin{displaymath} {\hbox{\tt K}} \to {\hbox{\tt L}}\,{\hbox{\tt t}}\,{\hbox{\t... ... 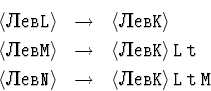{\hbox{\tt N}} --- нетерминалы, {\hbox{\tt t}} --- терминал),}\end{displaymath}в новую грамматику мы добавим правила \begin{eqnarray*} \langle{\hbox{\rm Лев}}{\hbox{\tt L}}\rangle& \to & \langle{\h... ...ox{\tt K}}\rangle\,{\hbox{\tt L}}\,{\hbox{\tt t}}\,{\hbox{\tt M}}\end{eqnarray*}и аналогично поступим с другими правилами. Смысл новых правил таков: пустое слово может появиться слева от P; если слово X может появиться слева от K, то X может появиться слева от L, XLt может появиться слева от M, XLtM -- слева от N. Индукцией по длине правого вывода легко проверить, что все, что может появиться слева от какого-то нетерминала, появляется в соответствии с этими правилами.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.7. Почему в предыдущей задаче важно, что мы рассматриваем только правые выводы?

Ответ. В противном случае следовало бы учитывать преобразования, происходящие внутри слова, стоящего слева от K.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 14.1.8. Для данной грамматики построить алгоритм, который по любому слову выясняет, каким из множеств ${\hbox{\tt Лев}}({\hbox{\tt K}})$ оно принадлежит.

(Замечание для знатоков. Существование такого алгоритма -- и даже конечного автомата, то есть индуктивного расширения с конечным числом значений, см. 1.3, -- вытекает из предыдущей задачи, так как построенная в ней грамматика имеет специальный вид: в правых частях всего один нетерминал, причем он стоит у левого края. Тем не менее мы приведем явное построение.)

Решение. Будем называть ситуацией данной грамматики одно из   ее правил, в правой части которого отмечена одна из позиций (до первой буквы, между первой и второй буквой,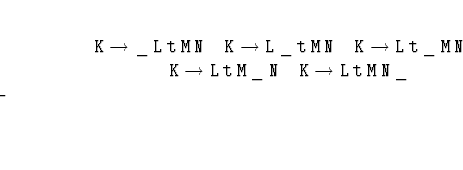 $\ldots$ , после последней буквы). Например, правило \begin{displaymath} {\hbox{\tt K}}\,\to\,{\hbox{\tt L}}\,{\hbox{\tt t}}\,{\hbox{\tt M}}\,{\hbox{\tt N}}\end{displaymath}(K, L, M, N -- нетерминалы, t -- терминал) порождает пять ситуаций: \begin{displaymath} \displaylines{ {\hbox{\tt K}}\to\_\,{\hbox{\tt L}}\,{\hbox{... ...ox{\tt L}}\,{\hbox{\tt t}}\,{\hbox{\tt M}}\,{\hbox{\tt N}}\,\_}\end{displaymath}(позиция указывается знаком подчеркивания).

Будем говорить, что слово S согласовано с ситуацией ${\hbox{\tt K}}\to{\hbox{\tt U}}\,\_{\hbox{\tt V}}$, если S кончается на U, то есть ${\hbox{\tt S}}={\hbox{\tt T}}{\hbox{\tt U}}$ при некотором T, и, кроме того, T принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$. (Смысл этого определения примерно таков: в стеке S подготовлена часть U для будущей свертки UV в K.) В этих терминах ${\hbox{\rm ЛевКонт}}({\hbox{\tt K}}\to{\hbox{\tt X}})$ -- это множество всех слов, согласованных с ситуацией ${\hbox{\tt K}}\to{\hbox{\tt X}}\,\_\,$, а ${\hbox{\rm Лев}}({\hbox{\tt К}})$ -- это множество всех слов, согласованных с ситуацией ${\hbox{\tt K}}\to\_\,{\hbox{\tt X}}$ (где ${\hbox{\tt K}}\to\_\,{\hbox{\tt X}})$ -- любое правило для нетерминала K).

Эквивалентное определение в терминах LR-процесса: S согласовано с ситуацией ${\hbox{\tt K}}\to{\hbox{\tt U}}\,\_\,{\hbox{\tt V}}$, если существует успешный LR-процесс, в котором события развиваются так:


$\scriptstyle{\blacktriangleright}$ 14.1.9. Доказать эквивалентность этих определений.

[Указание. Если ${\hbox{\tt S}} ={\hbox{\tt TU}}$ и T принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$, то можно получить в стеке сначала T, потом U, потом V, потом свернуть UV в K и затем успешно завершить процесс. (Мы используем несколько раз тот факт, что из любого нетерминала что-то да выводится: благодаря этому мы можем добавить в стек любое слово.)]$\blacktriangleleft$


Наша цель -- построение алгоритма, распознающего принадлежность произвольного слова к ${\hbox{\rm Лев}}({\hbox{\tt K}})$.Рассмотрим функцию, сопоставляющую с каждым словом S (из терминалов и нетерминалов) множество всех согласованных с ним ситуаций. Это множество назовем состоянием, соответствующим слову S.  Будем обозначать его ${\hbox{\rm Сост}}({\hbox{\tt S}})$. Достаточно показать, что функция ${\hbox{\rm Сост}}({\hbox{\tt S}})$ индуктивна, то есть что значение ${\hbox{\rm Сост}}({\hbox{\tt SJ}})$, где J -- терминал или нетерминал, может быть вычислено, если известно ${\hbox{\rm Сост}}({\hbox{\tt S}})$ и символ J. (Мы видели ранее, как принадлежность к ${\hbox{\rm Лев}}({\hbox{\tt К}})$ выражается в терминах этой функции.) Значение ${\hbox{\rm Сост}}({\hbox{\tt SJ}})$ вычисляется по таким правилам:

(1) Если слово S согласовано с ситуацией ${\hbox{\tt K}}\to{\hbox{\tt U}}\,\_\,{\hbox{\tt V}}$, причем слово V начинается на букву J, то есть ${\hbox{\tt V}}={\hbox{\tt JW}}$, то SJ согласовано с ситуацией ${\hbox{\tt K}}\to{\hbox{\tt UJ}}\,\_\,{\hbox{\tt W}}$.

Это правило полностью определяет все ситуации с непустой левой половиной (то есть не начинающиеся с подчеркивания), согласованные с SJ. Осталось определить, для каких нетерминалов K слово SJ принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$.Это делается по двум правилам:

(2) Если ситуация ${\hbox{\tt L}}\to{\hbox{\tt U}}\,\_\,{\hbox{\tt V}}$ согласована с SJ (согласно правилу (1)), а V начинается на нетерминал К, то SJ принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$.

(3) Если SJ входит в ${\hbox{\rm Лев}}({\hbox{\tt L}})$для некоторого L, причем ${\hbox{\tt L}}\to{\hbox{\tt V}}$ -- правило грамматики и V начинается на нетерминал K, то SJ принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$.

Заметим, что правило (3) можно рассматривать как аналог правила (2): в указанных в (3) предположениях ситуация ${\hbox{\tt L}}\to\_{\hbox{\tt V}}$ согласована с SJ, а V начинается на нетерминал K.

Корректность этих правил в общем-то очевидна, если хорошенько подумать. Единственное, что требует некоторых пояснений -- это то, почему с помощью правил (2) и (3) обнаружатся все терминалы K, для которых SJ принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$. Попытаемся это объяснить. Рассмотрим правый вывод, в котором SJ стоит слева от K. Откуда мог взяться в нем нетерминал K? Если правило, которое его породило, породило также и конец слова SJ, то принадлежность SJ к ${\hbox{\rm Лев}}({\hbox{\tt K}})$ будет обнаружена по правилу (2). Если же K было первой буквой слова, порожденного каким-то другим нетерминалом L, то -- благодаря правилу (3) -- достаточно установить принадлежность SJ к ${\hbox{\rm Лев}}({\hbox{\tt L}})$. Осталось применить те же рассуждения к L и так далее.

В терминах LR-процесса то же самое можно сказать так. Сначала нетерминал K может участвовать в нескольких свертках, не затрагивающих SJ (они соответствуют применению правила (3)), но затем он обязан подвергнуться свертке, затрагивающей SJ (что соответствует применению правила (2)).

Осталось выяснить, какие ситуации согласованы с пустым словом, то есть для каких нетерминалов K пустое слово принадлежит ${\hbox{\rm Лев}}({\hbox{\tt K}})$. Это определяется по следующим правилам:

(1) начальный нетерминал таков;

(2) если K таков и ${\hbox{\tt K}}\to {\hbox{\tt V}}$ -- правило грамматики, причем слово V начинается с нетерминала L, то и L таков.


$\scriptstyle{\blacktriangleright}$ 14.1.10. Проделать описанный анализ для грамматики

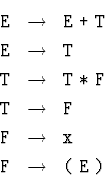\begin{eqnarray*} {\hbox{\tt E}}&\to& {\hbox{\tt E}}\;{\hbox{\tt +}}\;{\hbox{\tt... ...\hbox{\tt F}}&\to& {\hbox{\tt (}}\;{\hbox{\tt E}}\;{\hbox{\tt )}}\end{eqnarray*} (задающей тот же язык, что и грамматика примера 3, с. [*]).

Решение. Множества Сост(S) для различных S приведены в таблице.
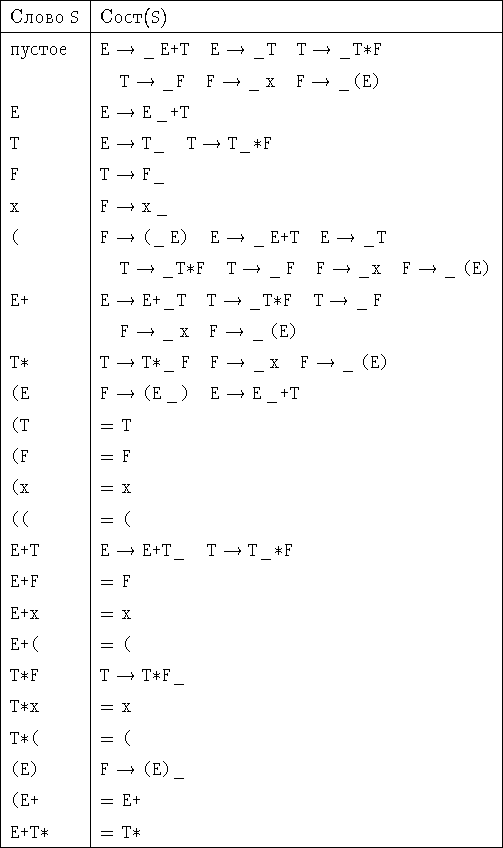
\begin{figure} {\begin{displaymath} \begin{tabular} {\vert l\vert l\vert} \hlin... ...+T*}}& = {\hbox{\tt T*}}\\ \hline\end{tabular}\end{displaymath}\par}\end{figure}

Знак равенства означает, что множества ситуаций, являющиеся значениями функции ${\hbox{\rm Сост}}({\hbox{\tt S}})$ на словах, стоящих слева и справа от знака равенства, одинаковы.

Правило определения ${\hbox{\rm Сост}}({\hbox{\tt SJ}})$, если известны ${\hbox{\rm Сост}}({\hbox{\tt S}})$ и J (здесь S -- слово из терминалов и нетерминалов, J -- терминал или нетерминал), таково:

надо найти ${\hbox{\rm Сост}}({\hbox{\tt S}})$ в правой колонке, взять соответствующее ему слово T в левой колонке, приписать к нему J и взять множество, стоящее напротив слова ТJ (если слово ТJ в таблице отсутствует, то ${\hbox{\rm Сост}}({\hbox{\tt SJ}})$пусто).$\scriptstyle\blacktriangleleft$


pvv
1/8/1999