Алгоритм разбора
для LL(1)-грамматик

В этом разделе мы рассмотрим еще один метод проверки выводимости в КС-грамматике, называемый по традиции     LL(1)-разбором. Вот его идея в одной фразе: можно считать, что в процессе вывода мы всегда заменяем самый левый нетерминал и нужно лишь выбрать одно из правил; если нам повезет с грамматикой, то выбрать правило можно, глядя на первый символ выводимого из этого нетерминала слова. Говоря более формально, дадим такое

13.3.1. Для каждого выводимого слова (из терминалов) существует его левый вывод.

13.3.2. В грамматике с 4 правилами найти левый вывод слова и доказать, что он единствен.

Что требуется от грамматики, чтобы такой метод поиска левого вывода был применим? Пусть, например, на очередном шаге самым левым нетерминалом оказался нетерминал K , т.е. мы имеем слово вида AKU , где A -- слово из терминалов, а U -- слово из терминалов и нетерминалов. Пусть в грамматике есть правила 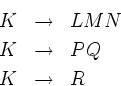Нам надо выбрать одно из них. Мы будем пытаться сделать этот выбор, глядя на первый символ той части входного слова, которая выводится из KU .

Рассмотрим множество Нач(LMN ) тех терминалов, с которых   начинаются непустые слова, выводимые из LMN . (Это множество равно Нач(L ), объединенному с Нач(M ), если из L выводится пустое слово, а также с Нач(N ), если из L и из M выводится пустое слово.) Чтобы описанный метод был применим, надо, чтобы Нач(LMN ), Нач(PQ ) и Нач(R ) не пересекались. Но этого мало. Ведь может быть так, например, что из LMN будет выведено пустое слово, а из слова U будет выведено слово, начинающееся на букву из Нач(PQ ). Следующие определения учитывают эту проблему.

Напомним, что определение выводимости в КС-грамматике было дано только для слова из терминалов. Оно очевидным образом обобщается на случай слов из терминалов и нетерминалов. Можно также говорить о выводимости одного слова (содержащего терминалы и нетерминалы) из другого. (Если говорится о выводимости слова без указания того, откуда оно выводится, то всегда подразумевается выводимость в грамматике, т.е. выводимость из начального нетерминала.)

Для каждого слова X из терминалов и нетерминалов через Нач(X ) обозначаем множество всех терминалов, с которых начинаются непустые слова из терминалов, выводимые из X . (В случае, если из любого нетерминала выводится хоть одно слово из терминалов, не играет роли, рассматриваем ли мы при определении Нач(X ) слова только из терминалов или любые слова. Мы будем предполагать далее, что это условие выполнено.)

Для каждого нетерминала K через Послед(K )   обозначим множество терминалов, которые встречаются в выводимых (в грамматике) словах сразу же за K . (Не смешивать с Посл(K ) предыдущего раздела!) Кроме того, в Послед(K ) включается символ EOI, если существует выводимое слово, оканчивающееся на K .

Для каждого правила (где K -- нетерминал, V -- слово, содержащее терминалы и нетерминалы) определим множество направляющих терминалов,         обозначаемое Напр(). По определению оно равно Нач(V ), к которому добавлено Послед(K ), если из V выводится пустое слово.

13.3.3. Является ли грамматика 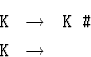(выводимыми словами являются последовательности диезов) LL(1)-грамматикой?

13.3.4. Написать LL(1)-грамматику для того же языка.

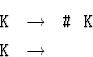Как говорят, << леворекурсивное>> правило заменено на << праворекурсивное>>.

Следующая задача показывает, что для LL(1)-грамматики существует не более одного возможного продолжения левого вывода.

13.3.5. Пусть дано выводимое в LL(1)-грамматике слово X , в котором выделен самый левый нетерминал K : X=AKS , где A -- слово из терминалов, S -- слово из терминалов и нетерминалов. Пусть существуют два различных правила грамматики с нетерминалом K в левой части, и мы применили их к выделенному в X нетерминалу K , затем продолжили вывод и в конце концов получили два слова из терминалов, начинающихся на A . Доказать, что в этих словах за началом A идут разные буквы. (Здесь к числу букв мы относим EOI.)

13.3.6. Доказать, что если слово выводимо в LL(1)-грамматике, то его левый вывод единствен.

13.3.7. Грамматика называется леворекурсивной, если из некоторого нетерминала K выводится слово, начинающееся с K , но не совпадающее с ним. Доказать, что леворекурсивная грамматика, в которой из каждого нетерминала выводится хотя бы одно непустое слово из терминалов и для каждого нетерминала существует вывод (начинающийся с начального нетерминала), в котором он встречается, не является LL(1)-грамматикой.

Таким образом, к леворекурсивным грамматикам (кроме тривиальных случаев) LL(1)-метод неприменим. Их приходится преобразовывать к эквивалентным LL(1)-грамматикам -- или пользоваться другими методами распознавания.

13.3.8. Используя сказанное, построить алгоритм проверки выводимости слова из терминалов в LL(1)-грамматике.

1.

слово AS выводимо в грамматике;

2.

любой левый вывод входного слова проходит через стадию AS

Вначале A пусто, а S состоит из единственного символа -- начального нетерминала.

Если в некоторый момент S начинается на терминал t и , то можно выполнить команду Move и удалить символ t, являющийся начальным в S, поскольку при этом AS не меняется.

Если S начинается на терминал t и , то входное слово невыводимо -- ибо по условию любой его вывод должен проходить через AS. (Это же справедливо и в случае .)

Если S пусто, то из условия (И) следует, что входное слово выводимо тогда и только тогда, когда .

Остается случай, когда S начинается с некоторого нетерминала K. По доказанному выше все левые выводы из S слов, начинающихся на символ Next, начинаются с применения к S одного и того же правила -- того, для которого Next принадлежит направляющему множеству. Если таких правил нет, то входное слово невыводимо. Если такое правило есть, то нужно применить его к первому символу слова S -- при этом свойство (И) не нарушится. Приходим к такому алгоритму:

 S := пустое слово;
 error := false;
 {error => входное слово невыводимо;}
 {not error => (И)}
 while (not error) and not ((Next=EOI) and (S пусто))
 | |  do begin
 | if (S начинается на терминал, равный Next) then begin
 | | Move; удалить из S первый символ;
 | end else if (S начинается на терминал, не равный Next)
 | |           then begin
 | | error := true;
 | end else if (S пусто) and (Next <> EOI) then begin
 | | error := true;
 | end else if (S начинается на нетерминал и Next входит в
 | |    направляющее множество одного из правил для этого
 | |    нетерминала) then begin
 | | применить это правило
 | end else if (S начинается на нетерминал и Next не входит
 | |  в направляющее множество ни одного из правил для этого
 | |  нетерминала) then begin
 | | error := true;
 | end else begin
 | | {так не бывает}
 | end;
 end;
 {входное слово выводимо <=> not error}

Замечания

• Приведенный алгоритм использует S как стек (все действия производятся с левого конца).
• Действия двух последних вариантов внутри цикла не приводят к чтению очередного символа со входа, поэтому их можно заранее предвычислить для каждого нетерминала и каждого символа Next. После этого на каждом шаге цикла будет читаться очередной символ входа.
• При практической реализации удобно составить таблицу, в которой записаны варианты действий в зависимости от входного символа и первого символа S, и небольшую программу, выполняющую действия в соответствии с этой таблицей.

13.3.9.  При проверке того, относится ли данная грамматика к типу LL(1), необходимо вычислить Послед(T ) и Нач(T ) для всех нетерминалов T . Как это сделать?