Метод рекурсивного спуска

В отличие от алгоритма предыдущего раздела (представляющего чисто теоретический интерес), алгоритмы на основе рекурсивного     спуска часто используются на практике. Этот метод применим, однако, далеко не ко всем грамматикам. Мы обсудим необходимые ограничения позднее.

Идея метода рекурсивного спуска такова. Для каждого нетерминала K мы строим процедуру ReadK, которая -- в применении к любому входному слову x -- делает две вещи:

Прежде чем описывать этот метод более подробно, договоримся о том, как процедуры получают сведения о входном слове и как сообщают о результатах своей работы. Мы предполагаем, что буквы входного слова поступают к ним по одной, т.е. имеется граница, отделяющая << прочитанную>> часть от << непрочитанной>>. Будем считать, что есть функция (без параметров)

Next: Symbol
дающая первый непрочитанный символ. Ее значениями могут быть терминальные символы, а также специальный символ EOI (End Of Input -- конец входа), означающий, что все слово уже прочитано. Вызов этой функции, разумеется, не сдвигает границы между прочитанной и непрочитанной частью -- для этого есть процедура Move, которая сдвигает границу на один символ. (Она применима, если Next<>EOI.) Пусть, наконец, имеется булевская переменная b.

Теперь мы можем сформулировать наши требования к процедуре ReadK. Они состоят в следующем:

Для удобства введем такую терминологию: выводимое из K слово будем называть K-словом, а любое начало любого выводимого из K слова -- K-началом. Два сформулированных требования вместе будем выражать словами <<ReadK корректна для K>>.

Начнем с примера. Пусть правило

K $\to$ L M
является единственным правилом грамматики, содержащим K в левой части, пусть L, M -- нетерминалы и ReadL, ReadM -- корректные (для них) процедуры.

Рассмотрим такую процедуру: 

     procedure ReadK;
     begin
     | ReadL;
     | if b then begin
     | | ReadM;
     | end;
     end;


$\scriptstyle{\blacktriangleright}$ 13.2.1. Привести пример, когда эта процедура будет некорректной для K.

Ответ. Пусть из L выводится любое слово вида 00..00, а из M выводится лишь слово 01. Тогда из K выводится слово 00001, но процедура ReadK этого не заметит.$\scriptstyle\blacktriangleleft$

Укажем достаточные условия корректности процедуры
ReadK. Для этого нам понадобятся некоторые обозначения. Пусть фиксированы КС-грамматика и некоторый нетерминал N этой грамматики. Рассмотрим N -слово A , которое имеет собственное начало B , также являющееся N -словом (если такие есть). Для любой пары таких слов A и B рассмотрим терминальный символ, идущий в A непосредственно за B . Множество всех таких терминалов обозначим   Посл(N ). (Если никакое N -слово не является собственным началом другого N -слова, то множество Посл(N ) пусто.)


$\scriptstyle{\blacktriangleright}$ 13.2.2. Указать (а) Посл(E) для примера 1 (с. [*]); (б) Посл(E) и Посл(T) для примера 2 (с. [*]); (в) Посл(33003) и Посл(33004) для примера 3 (с. [*]);

Ответ. (а) Посл(E) = $\{ \hbox{\tt [}, \hbox{\tt (}\}$.(б) Посл(E) = $\{ \hbox{\tt [}, \hbox{\tt (}\}$;Посл(T) пусто (никакое T-слово не является началом другого).
(в) Посл(33005) = $\{\hbox{\tt *}\}$; Посл(33006) пусто.$\scriptstyle\blacktriangleleft$

Кроме того, для каждого нетерминала N обозначим через Нач(N )  множество всех терминалов, являющихся первыми буквами непустых N -слов. Это обозначение -- вместе с предыдущим -- позволит дать достаточное условие корректности процедуры ReadK в описанной выше ситуации.


$\scriptstyle{\blacktriangleright}$ 13.2.3. Доказать, что если Посл(L) не пересекается с Нач(M) и множество всех M-слов непусто, то ReadK корректна.

Решение. Рассмотрим два случая.

(1) Пусть после ReadL значение переменной b ложно. В этом случае ReadL читает со входа максимальное L-начало A , не являющееся L-словом. Оно является K-началом (здесь важно, что множество M-слов непусто.). Будет ли оно максимальным K-началом среди начал входа? Если нет, то A является началом слова BC , где B есть L-слово, C есть M-начало и BC -- более длинное начало входа, чем A . Если B длиннее A , то A -- не максимальное начало входа, являющееся L-началом, что противоречит корректности ReadL. Если B = A , то A было бы L-словом, а это не так. Значит, B короче A , C непусто и первый символ слова C следует в A за последним символом слова B , т.е. Посл(L) пересекается с Нач(M). Противоречие. Итак, A максимально. Из сказанного следует также, что A не является K-словом. Корректность процедуры ReadK в этом случае проверена.

(2) Пусть после ReadL значение переменной b истинно. Тогда прочитанное процедурой ReadK начало входа имеет вид AB , где A есть L-слово, а B есть M-начало. Тем самым AB есть K-начало. Проверим его максимальность. Пусть C есть большее K-начало. Тогда либо C есть L-начало (что невозможно, так как A было максимальным L-началом), либо C = A'B' , где A' -- L-слово, B' -- M-начало. Если A' короче A , то B' непусто и начинается с символа, принадлежащего и Нач(M), и Посл(L), что невозможно. Если A' длиннее A , то A -- не максимальное L-начало. максимальным. Итак, A' = A . Но в этом случае B' есть продолжение B , что противоречит корректности ReadM. Итак, AB -- максимальное K-начало. Остается проверить правильность выдаваемого процедурой ReadK значения переменной b. Если оно истинно, то это очевидно. Если оно ложно, то B не есть M-слово, и надо проверить, что AB -- не K-слово. В самом деле, если бы выполнялось AB = A'B' , где A' -- L-слово, B' -- M-слово, то A' не может быть длиннее A (ReadL читает максимальное слово), A' не может быть равно A (тогда B' равно B и не является M-словом) и A' не может быть короче A (тогда первый символ B' принадлежит и Нач(M), и Посл(L)). Задача решена.$\scriptstyle\blacktriangleleft$

Перейдем теперь к другому частному случаю. Пусть в КС-грамматике есть правила 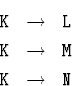\begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt L}\\ \hbox{\tt K}&\to&\hbox{\tt M}\\ \hbox{\tt K}&\to&\hbox{\tt N}\end{eqnarray*}и других правил с левой частью K нет.


$\scriptstyle{\blacktriangleright}$ 13.2.4. Считая, что ReadL, ReadM и ReadN корректны (для L, M и N) и что множества Нач(L), Нач(M) и Нач(N) не пересекаются, написать процедуру, корректную для K.

Решение. Схема процедуры такова: 
     procedure ReadK;
     begin
     | if (Next принадлежит Нач(L)) then begin
     | | ReadL;
     | end else if (Next принадлежит Нач(M)) then begin
     | | ReadM;
     | end else if (Next принадлежит Нач(N)) then begin
     | | ReadN;
     | end else begin
     | | b := true или false  в зависимости от того,
     | |      выводимо ли пустое слово из K или нет
     | end;
     end;
Докажем, что ReadK корректно реализует K. Если Next не принадлежит ни одному из множеств Нач(L), Нач(M), Нач(N),то пустое слово является наибольшим началом входа, являющимся K-началом. Если Next принадлежит одному (и, следовательно, только одному) из этих множеств, то максимальное начало входа, являющееся K-началом, непусто и читается соответствующей процедурой.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 13.2.5. Используя сказанное, составьте процедуру распознавания выражений для грамматики (пример 3, с. [*]): \begin{eqnarray*} \vyrazh &\to&\slag \ \ostvyr \\ \ostvyr &\to& \hbox{\tt +}\ \... ... \hbox{\tt x}\\ \mnozh &\to& \hbox{\tt(}\ \vyrazh \ \hbox{\tt )}\end{eqnarray*}

Решение. Эта грамматика не полностью подпадает под рассмотренные частные случаи: в правых частях есть комбинации терминалов и нетерминалов
+ 32998
и группы из трех символов
( 32999 )
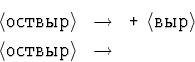В грамматике есть также несколько правил с одной левой частью и с правыми частями разного рода, например \begin{eqnarray*} \ostvyr &\to& \hbox{\tt +}\ \vyrazh \\ \ostvyr &\to&\end{eqnarray*}Эти ограничения не являются принципиальными. Так, правило типа 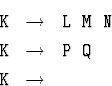$\hbox{\tt K}\to \hbox{\tt L M N}$можно было бы заменить на два правила $\hbox{\tt K} \to \hbox{\tt L Q}$ и $\hbox{\tt Q} \to \hbox{\tt M N}$, терминальные символы в правой части -- на нетерминалы (с единственным правилом замены на соответствующие терминалы). 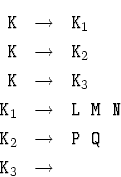Несколько правил с одной левой частью и разнородными правыми также можно свести к уже разобранному случаю: например, \begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt L M N}\\ \hbox{\tt K}&\to&\hbox{\tt P Q}\\ \hbox{\tt K}&\to&\end{eqnarray*}можно заменить на правила \begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt K}_1\\ \hbox{\tt K}&\to&\hbox{\tt K... ... M N}\\ \hbox{\tt K}_2 &\to&\hbox{\tt P Q}\\ \hbox{\tt K}_3 &\to&\end{eqnarray*}Но мы не будем этого делать -- а сразу же запишем то, что получится, если подставить описания процедур для новых терминальных символов в места их использования. Например, для правила \begin{displaymath} \hbox{\tt K} \to \hbox{\tt L M N}\end{displaymath}это дает процедуру 
        procedure ReadK;
        begin
        | ReadL;
        | if b then begin ReadM; end;
        | if b then begin ReadN; end;
        end;
Для ее корректности надо, чтобы Посл(L) не пересекалось с Нач(MN) (которое равно Нач(M), если из M не выводится пустое слово, и равно объединению Нач(M) и Нач(N), если выводится), а также чтобы Посл(M) не пересекалось с Нач(N).

Аналогичным образом правила 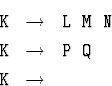\begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt L M N}\\ \hbox{\tt K}&\to&\hbox{\tt P Q}\\ \hbox{\tt K}&\to&\end{eqnarray*}приводят к процедуре 

        procedure ReadK;
        begin
        | if (Next принадлежит Нач(LMN)) then begin
        | | ReadL;
        | | if b then begin ReadM; end;
        | | if b then begin ReadN; end;
        | end else if (Next принадлежит Нач(PQ)) then begin
        | | ReadP;
        | | if b then begin ReadQ; end;
        | end else begin
        | | b := true;
        | end;
        end;
корректность которой требует, чтобы Нач(LMN) не пересекалось с Нач(PQ).

Читая приведенную далее программу, полезно иметь в виду соответствие между русскими и английскими словами: \begin{displaymath} \begin{tabular} {ll} ВЫРажение & {\hbox{\cmrfont EXPRession... ...ive term}}\\ МНОЖитель & {\hbox{\cmrfont FACTor}}\end{tabular}\end{displaymath}

     procedure ReadSymb (c: Symbol);
     | b := (Next = c);
     | if b then begin Move; end;
     end;

     procedure ReadExpr;
     | ReadAdd;
     | if b then begin ReadRestExpr; end;
     end;

     procedure ReadRestExpr;
     | if Next = '+' then begin
     | | ReadSymb ('+');
     | | if b then begin ReadExpr; end;
     | end else begin
     | | b := true;
     | end;
     end;

     procedure ReadAdd;
     | ReadFact;
     | if b then begin ReadRestAdd; end;
     end;

     procedure ReadRestAdd;
     | if Next = '*' then begin
     | | ReadSymb ('*');
     | | if b then begin ReadAdd; end;
     | end else begin
     | | b := true;
     | end;
     end;

     procedure ReadFact;
     | if Next = 'x' then begin
     | | ReadSymb ('x');
     | end else if Next = '(' then begin
     | | ReadSymb ('(');
     | | if b then begin ReadExpr; end;
     | | if b then begin ReadSymb (')'); end;
     | end else begin
     | | b := false;
     | end;
     end;
Осталось обсудить проблемы, связанные с взаимной рекурсивностью этих процедур (одна использует другую и наоборот). В паскале это допускается, только требуется дать предварительное описание процедур (<< forward>>). Как всегда для рекурсивных процедур, помимо доказательства того, что каждая процедура работает правильно в предположении, что используемые в ней вызовы процедур работают правильно, надо доказать отдельно, что работа завершается. (Это не очевидно: если в грамматике есть правило $\hbox{\tt K}\to\hbox{\tt KK}$, то из K ничего не выводится, Посл(K) и Нач(K) пусты, но написанная по нашим канонам процедура 
     procedure ReadK;
     begin
     | ReadK;
     | if b then begin
     | | ReadK;
     | end;
     end;
не заканчивает работы.)

В даннном случае процедуры ReadRestExpr, ReadRestAdd, ReadFact либо завершаются, либо уменьшают длину непрочитанной части входа. Поскольку любой цикл вызовов включает одну из них, то зацикливание невозможно. Задача решена.$\scriptstyle\blacktriangleleft$


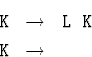$\scriptstyle{\blacktriangleright}$ 13.2.6. Пусть в грамматике имеются два правила с нетерминалом K в левой части, имеющих вид \begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt L K}\\ \hbox{\tt K}&\to&\end{eqnarray*}по которым K-слово представляет собой конечную последовательность L-слов, причем множества Посл(L) и Нач(K) (в данном случае равное Нач(L)) не пересекаются. Используя корректную для L процедуру ReadL, написать корректную для K процедуру ReadK, не используя рекурсии. Предполагается, что пустое слово не выводимо из L.

Решение. По нашим правилам следовало бы написать 
     procedure ReadK;
     begin
     | if (Next принадлежит Нач(L)) then begin
     | | ReadL;
     | | if b then begin ReadK; end;
     | end else begin
     | | b := true;
     | end;
     end;
завершение работы гарантируется тем, что пустое слово не выводимо из L (и, следовательно, перед рекурсивным вызовом длина непрочитанной части уменьшается).

Эта рекурсивная процедура эквивалентна нерекурсивной: 

     procedure ReadK;
     begin
     | b := true;
     | while b and (Next принадлежит Нач(L)) do begin
     | | ReadL;
     | end;
     end;
Формально можно проверить эту эквивалентность так. Завершаемость в обоих случаях ясна. Достаточно проверить поэтому, что тело рекурсивной процедуры эквивалентно нерекурсивной в предположении, что ее рекурсивный вызов эквивалентен вызову нерекурсивной процедуры. Подставим: 
     if (Next принадлежит Нач(L)) then begin
     | ReadL;
     | if b then begin
     | | b := true;
     | | while b and (Next принадлежит Нач(L)) do begin
     | | | ReadL;
     | | end;
     | end;
     end else begin
     | b := true;
     end;
Первую команду b:=true можно выкинуть (в этом месте и так b истинно). Вторую команду можно перенести в начало: 
     b := true;
     if (Next принадлежит Нач(L) then begin
     | ReadL;
     | if b then begin
     | | while b and (Next принадлежит Нач(L)) do begin
     | | | ReadL;
     | | end;
     | end;
     end;
Теперь внутренний if можно выкинуть (если b ложно, цикл while все равно не выполняется) и добавить в условие внешнего if условие b (которое все равно истинно). 
     b := true;
     if b and (Next принадлежит Нач(L)) then begin
     | ReadL;
     | while b and (Next принадлежит Нач(L)) do begin
     | | ReadL;
     | end;
     end;
что эквивалентно приведенной выше нерекурсивной процедуре (из которой вынесена первая итерация цикла).$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 13.2.7. Доказать корректность приведенной выше нерекурсивной программы непосредственно, без ссылок на рекурсивную.

Решение. Рассмотрим наибольшее начало входа, являющееся K-началом. Оно представляется в виде конкатенации (последовательного приписывания) нескольких непустых L-слов и, возможно, одного непустого L-начала, не являющегося L-словом. Инвариант цикла: прочитано несколько из них; b $\Leftrightarrow$ (последнее прочитанное является L-словом).

Сохранение инварианта: если осталось последнее слово, это очевидно; если осталось несколько, то за первым L-словом (из числа оставшихся) идет символ из Нач(L), и потому это слово -- максимальное начало входа, являющееся L-началом.$\scriptstyle\blacktriangleleft$

На практике при записи грамматики используют сокращения. Если правила для какого-то нетерминала K имеют вид 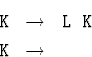\begin{eqnarray*} \hbox{\tt K}&\to&\hbox{\tt L K}\\ \hbox{\tt K}&\to&\end{eqnarray*}(т.е. K-слова -- это последовательности L-слов), то этих правил не пишут, а вместо K пишут L в фигурных скобках. Несколько правил с одной левой частью и разными правыми записывают как одно правило, разделяя альтернативные правые части вертикальной чертой.

Например, рассмотренная выше грамматика для 33008 может быть записана так: \begin{eqnarray*} \vyrazh &\to& \slag \hbox{ \tt \{ + \slag \ \}}\\ \slag &\to&... ...\mnozh \ \}}\\ \mnozh &\to& \hbox{ \tt x}\ \vert\ (\ \vyrazh \ )\end{eqnarray*}


$\scriptstyle{\blacktriangleright}$ 13.2.8. Написать процедуру, корректную для 33009, следуя этой грамматике и используя цикл вместо рекурсии, где можно.

Решение: 

     procedure ReadSymb (c: Symbol);
     | b := (Next = c);
     | if b then begin Move; end;
     end;

     procedure ReadExpr;
     begin
     | ReadAdd;
     | while b and (Next = '+') do begin
     | | Move; ReadAdd;
     | end;
     end;

     procedure ReadAdd;
     begin
     | ReadFact;
     | while b and (Next = '*') do begin
     | | Move; ReadFact;
     | end;
     end;

     procedure ReadFact;
     begin
     | if Next = 'x' do begin
     | | Move; b := true;
     | end else if Next = '(' then begin
     | | Move; ReadExpr;
     | | if b then begin ReadSymb (')'); end;
     | end else begin
     | | b := false;
     | end;
     end;`


$\scriptstyle{\blacktriangleright}$ 13.2.9.  В последней процедуре команду b:=true можно опустить. Почему?

Решение. Можно предполагать, что все процедуры вызываются при b=true.$\scriptstyle\blacktriangleleft$

Алгоритм разбора для LL(1)-грамматик

pvv
1/8/1999