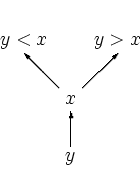
Каждое дерево будем считать представлением множества всех пометок на его вершинах. При этом одно и то же множество может иметь различные представления.
Благодаря упорядоченности каждый элемент может легко
<< найти свое место>> в дереве: придя в какую-то вершину и
сравнив себя с тем, кто там находится, элемент решает, идти ему
налево или направо.

Начав с корня и двигаясь по этому правилу, он либо обнаружит, что такой элемент уже есть, либо найдет место, в котором он должен быть.
Всюду далее мы предполагаем, что на значениях типа T задан порядок, и рассматриваем только упорядоченные деревья.