Полное двоичное дерево. T-деревья

  Нарисуем точку. Из нее проведем две стрелки (влево вверх и вправо вверх) в две другие точки. Из каждой из этих точек проведем по две стрелки и так далее. Полученную картинку (в n -ом слое будет 2n - 1 точек) называют полным двоичным деревом. Нижнюю точку называют корнем. У каждой вершины есть два   сына (две вершины, в которые идут стрелки) -- левый и правый. У всякой вершины, кроме корня, есть единственный отец.

Пусть выбрано некоторое конечное множество вершин полного двоичного дерева, содержащее вместе с каждой вершиной и всех ее предков. Пусть на каждой вершине этого множества написано значение фиксированного типа T (то есть задано отображение множества вершин в множество значений типа T ). То, что получится, будем называть T -деревом. Множество всех T -деревьев обозначим $\Tree (T)$.

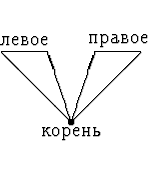
Рекурсивное определение. Всякое непустое T -дерево разбивается на три части: корень (несущий пометку из T ), левое и правое поддеревья (которые могут быть пустыми). Это разбиение устанавливает взаимно однозначное соответствие между множеством непустых T -деревьев и произведением $T \times \Tree (T) \times \Tree (T)$.Обозначив через empty пустое дерево, можно написать \begin{displaymath} \Tree (T) =\{{{\hbox{\cmrfont empty}}}\}+T\times\Tree (T)\times\Tree (T).\end{displaymath}\begin{displaymath} \setlength {\unitlength}{1em} \begin{picture} (8,6) \put(4... ...}}}} \put(5,5){\makebox(2,1){{\hbox{\rm правое}}}}\end{picture}\end{displaymath}



pvv
1/8/1999