Более сложные образцы
и автоматы

Более сложные образцы и автоматы

Мы можем искать не конкретное слово, а подслова заданного вида. Например, можно искать слова вида a?b, где вместо ? может стоять любая буква (иными словами, нас интересует буква b на расстоянии 2 после буквы a).

$\scriptstyle{\blacktriangleright}$ 10.7.1. Указать конечный автомат, проверяющий, есть ли во входном слове фрагмент вида a?b.

Решение. Читая слово, следует помнить, есть ли буква a на последнем месте и на предпоследнем -- пока не встретим искомый фрагмент. Автомат имеет состояния 00, 01, 10, 11, их смысл таков: $\begin{displaymath} \begin{tabular} {rl} 00& на предпоследнем и последнем местах... ...нем есть, на последнем нет\\ 11& есть и там, и там\end{tabular}\end{displaymath}$

1cm

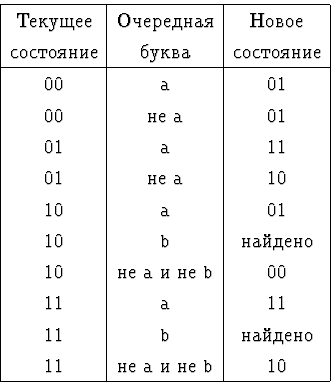
Таблица переходов автомата: $\begin{displaymath} \begin{tabular} {\vert c\vert c\vert c\vert} \hline Текущее... ... {\hbox{\tt a}} и не {\hbox{\tt b}} & 10 \\ \hline\end{tabular}\end{displaymath}$ $\scriptstyle\blacktriangleleft$

Другой стандартный знак в образце -- это звездочка (*), на место которой может быть подставлено любое слово. Например, образец ab*cd означает, что мы ищем подслово ab, за которым следует что угодно, а затем (на любом расстоянии) идет cd.

$\scriptstyle{\blacktriangleright}$ 10.7.2. Указать конечный автомат, проверяющий, есть ли во входном слове образец ab*cd (в описанном только что смысле).

Решение:

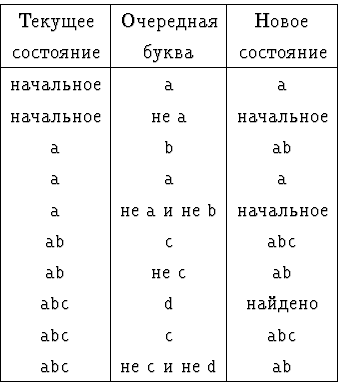
$\begin{displaymath} \begin{tabular} {\vert c\vert c\vert c\vert} \hline Текущее... ...}} и не {\hbox{\tt d}} & {\hbox{\tt ab}} \\ \hline\end{tabular}\end{displaymath}$ $\scriptstyle\blacktriangleleft$

Еще один вид поиска -- это поиск любого из слов некоторого списка.

$\scriptstyle{\blacktriangleright}$ 10.7.3. Дан список слов $X_1,\ldots,X_k$ и слово Y . Определить, входит ли хотя бы одно из слов X_i в слово Y (как подслово). Количество действий не должно превосходить константы, умноженной на суммарную длину всех слов (из списка и того, в котором происходит поиск).

Решение. Очевидный способ состоит в том, чтобы каждое слово из списка проверять отдельно (с помощью одного из рассмотренных алгоритмов). Однако при этом мы не укладываемся в заданное число действий (из-за умножения k на длину слова Y ).

Посмотрим на дело с другой стороны. Каждому образцу из списка соответствует конечный автомат с некоторым множеством состояний. Эти автоматы можно объединить в один, множеством состояний которого будет произведение множеств состояний всех тех автоматов. Это -- очень большое множество. Однако на самом деле большинство его элементов недоступны (не могут появиться при чтении входного слова) и за счет этого получается экономия. Примерно эту идею (но в измененном виде) мы и будем использовать.

Вспомним алгоритм Кнута-Морриса-Пратта. В нем, читая входное слово, мы хранили наибольшее начало образца, являющееся концом прочитанной части. Теперь нам следует хранить для каждого из образцов наибольшее его начало, являющееся концом прочитанной части. Решающим оказывается такое замечание: достаточно хранить самое длинное из них -- все остальные по нему восстанавливаются (как наибольшие начала образцов, являющиеся его концами).

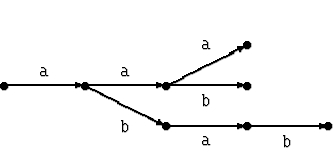Склеим все образцы в дерево, объединив их совпадающие начальные участки. Например, набору образцов $\begin{displaymath} \{{\hbox{\tt aaa}}, {\hbox{\tt aab}}, {\hbox{\tt abab}}\}\end{displaymath}$ соответствует дерево $\begin{displaymath} \begin{picture} (10,4) \thicklines \put(1,2){\circle*{... ...\put(7,3){\circle*{.15}} \put(9,1){\circle*{.15}}\end{picture}\end{displaymath}$ Формально говоря, вершинами дерева являются все начала всех образцов, а сыновья вершины получаются приписыванием буквы.

Читая входное слово, мы двигаемся по этому дереву: текущая вершина -- это наибольшая (самая правая) из вершин, являющихся концом прочитанной части (= наибольший конец прочитанной части, являющийся началом одного из образцов).

Определим функцию l , аргументами и значениями которой являются вершины дерева. Именно, l(P) = наибольшая вершина дерева, являющаяся концом P . (Напомним, вершины дерева -- это слова.) Нам понадобится такое утверждение:

$\scriptstyle{\blacktriangleright}$ 10.7.4. Пусть P -- вершина дерева. Докажите, что множество всех вершин, являющихся концами P , равно $\{l(P), l(l(P)),\ldots\}$

Решение. См. доказательство аналогичного утверждения для алгоритма Кнута-Морриса-Пратта. $\scriptstyle\blacktriangleleft$

Теперь ясно, что нужно делать, находясь в вершине P и читая букву z входного слова. Надо просматривать последовательно вершины P , l(P) , l(l(P)) ,..., пока не обнаружится такая, из которой выходит стрелка с буквой z. Та вершина, в которую эта стрелка ведет, и будет нашим следующим положением.

Остается понять, как для каждой вершины дерева вычислить указатель на значение функции l в этой вершине. Это делается как раньше, при этом значения l для более коротких слов используются при вычислении очередного значения функции l . Это означает, что вершины дерева следует просматривать в порядке возрастания их длины. Нетрудно понять, что все это можно уложить в требуемое число действий (хотя константа зависит от числа букв в алфавите). Относящиеся к этому подробности см. в главе 9. $\scriptstyle\blacktriangleleft$

Можно поинтересоваться, какие свойства слов распознаются с помощью конечных автоматов. Оказывается, что существует просто описываемый класс образцов, задающий все такие свойства -- класс регулярных выражений.

Определение. Пусть фиксирован конечный алфавит $\Gamma$ ,не содержащий символов $\Lambda$ , $\varepsilon$ , (, ), * и | (они будут использоваться для построения регулярных выражений и не должны перемешиваться с буквами). Регулярные выражения строятся по таким правилам:

(а): буква алфавита $\Gamma$ -- регулярное выражение;
(б): символы $\Lambda$ , $\varepsilon$ -- регулярные выражения;
(в): если $A,B,C,\ldots,E$ -- регулярные выражения, то
${\hbox{\tt (}}ABC\ldots E{\hbox{\tt )}}$ -- регулярное выражение;
(г): если $A,B,C,\ldots,E$ -- регулярные выражения, то
${\hbox{\tt (}}A{\hbox{\tt \vert}}B{\hbox{\tt \vert}}C{\hbox{\tt \vert}}\ldots{\hbox{\tt \vert}}E{\hbox{\tt )}}$ -- регулярное выражение;
(д): если A -- регулярное выражение, то $A{\hbox{\tt *}}$ -- регулярное выражение.

Каждое регулярное выражение задает множество слов в алфавите Г по таким правилам:

(а): букве соответствует одноэлементное множество, состоящее из однобуквенного слова, состоящего из этой буквы;
(б): символу $\varepsilon$ соответствует пустое множество, а символу $\Lambda$ -- одноэлементное множество, единственным элементом которого является пустое слово;
(в): регулярному выражению ${\hbox{\tt (}}ABC\ldots E{\hbox{\tt )}}$ соответствует множество всех слов, которые можно получить, если к слову из A приписать слово из B , затем из C ,..., затем из E (конкатенация множеств);
(г): регулярному выражению ${\hbox{\tt (}}A{\hbox{\tt \vert}}B{\hbox{\tt \vert}}C{\hbox{\tt \vert}}\ldots{\hbox{\tt \vert}}E{\hbox{\tt )}}$ соответствует объединение множеств, соответствующих выражениям $A,B,C,\ldots,E$ ;
(д): регулярному выражению $A{\hbox{\tt *}}$ соответствует итерация множества, соответствующего выражению A , то есть множество всех слов, которые можно так разрезать на куски, что каждый кусок принадлежит множеству, соответствующему выражению A . (В частности, пустое слово всегда содержится в $A{\hbox{\tt *}}$ .)

Множества, соответствующие регулярным выражениям, называются регулярными. Вот несколько примеров: $\begin{displaymath} \footnotesize \begin{tabular} {ll} Выражение & Множество \\ ... ...ы не более 2 из букв {\hbox{\tt a}},{\hbox{\tt b}}\end{tabular}\end{displaymath}$

$\scriptstyle{\blacktriangleright}$ 10.7.5. Написать регулярное выражение, которому соответствует множество всех слов из букв a и b, в которых число букв a четно.

Решение. Выражение b* задает все слова без буквы a, а выражение ${\hbox{\tt (b*}}\,{\hbox{\tt a}}\,{\hbox{\tt b*}}\,{\hbox{\tt a}}\,{\hbox{\tt b*)}}$ -- все слова ровно с двумя буквами a. Остается объединить эти множества, а потом применить итерацию: $\begin{displaymath} {\hbox{\tt (}}\,{\hbox{\tt (b*}}\,{\hbox{\tt a}}\,{\hbox{\tt... ... a}}\,{\hbox{\tt b*)}}\,\vert\,{\hbox{\tt b*}}\,{\hbox{\tt )*}}\end{displaymath}$ Другой вариант ответа: $\begin{displaymath} \hskip500cm minus500cm{\hbox{\tt (b*}}\,{\hbox{\tt a}}\,{\hb... ...ap{\kern.5em\hbox{\normalsize$\scriptstyle\blacktriangleleft$}}\end{displaymath}$

$\scriptstyle{\blacktriangleright}$ 10.7.6. Написать регулярное выражение, которое задает множество всех слов из букв ${\hbox{\tt a}},{\hbox{\tt b}},{\hbox{\tt c}}$ , в которых слово bac является подсловом.

Решение. ${\hbox{\tt ((a\vert b\vert c)*}}\,{\hbox{\tt bac}}\,{\hbox{\tt (a\vert b\vert c)*)}}$ $\scriptstyle\blacktriangleleft$

Теперь задачу о поиске образца в слове можно переформулировать так: проверить, принадлежит ли слово множеству, соответствующему данному регулярному выражению.

$\scriptstyle{\blacktriangleright}$ 10.7.7. Какие выражения соответствуют образцам a?b и ab*cd, рассмотренным ранее? (В образце символ * используется не в том смысле, что в регулярных выражениях!) Предполагается, что алфавит содержит буквы ${\hbox{\tt a}},{\hbox{\tt b}},{\hbox{\tt c}},{\hbox{\tt d}},{\hbox{\tt e}}$ .

Решение:

$\begin{displaymath} \displaylines {{\hbox{\tt ((a\vert b\vert c\vert d\vert e)*... ...p{\kern.5em\hbox{\normalsize$\scriptstyle\blacktriangleleft$}}}\end{displaymath}$

$\scriptstyle{\blacktriangleright}$ 10.7.8. Доказать, что для всякого регулярного выражения можно построить конечный автомат, который распознает соответствующее этому выражению множество слов.

Решение. Нам потребуется новое понятие -- понятие источника, или недетерминированного конечного автомата. Представим себе ориентированный граф -- картинку из нескольких точек (вершин) и некоторых стрелок, соединяющих эти точки (ребер). Пусть на некоторых ребрах написаны буквы (не обязательно на всех). Пусть также среди вершин выбраны две -- начальная Н и конечная К. Такая картинка называется источником.

Будем двигаться различными способами из Н в К, читая буквы по дороге (на тех стрелках, где они есть). Каждому пути из Н в К, таким образом, соответствует некоторое слово. А источнику в целом соответствует множество слов -- тех слов, которые можно прочесть на путях из Н в К.

Замечание. Если нарисовать состояния конечного автомата в виде точек, а переходы при чтении букв изобразить в виде стрелок, то станет ясно, что конечный автомат -- это частный случай источника. (С дополнительными требованиями: (а) на всех стрелках есть буквы, и (б) для любой точки на выходящих из нее стрелках каждая буква встречается ровно один раз.)

Мы будем строить конечный автомат по регулярному выражению в два приема. Сначала мы построим источник, которому соответствует то же самое множество слов. Затем для произвольного источника построим автомат, который проверяет, принадлежит ли слово соответствующему множеству.

$\scriptstyle{\blacktriangleright}$ 10.7.9. По регулярному выражению построить источник, задающий то же множество.

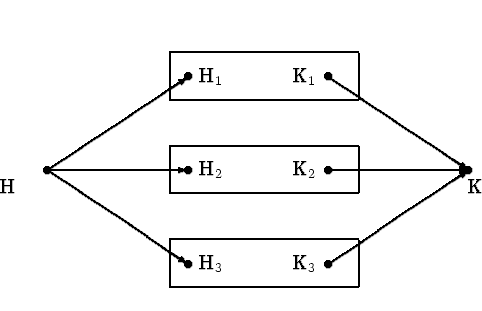Решение. Индукция по построению регулярного выражения. Буквам соответствуют графы из одной стрелки. Объединение реализуется так: $\begin{displaymath} { \setlength {\unitlength}{.032\textwidth} \thicklines ... ... \put(21,6){\circle*{.3}} \put(21,5){\makebox{К}}\end{picture}}\end{displaymath}$ Нарисована картинка для объединения трех множеств, прямоугольники -- это источники, им соответствующие; указаны начальные и конечные вершины. На новых стрелках (их 6 ) букв не написано.

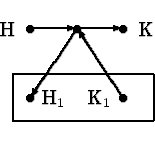
Конкатенации соответствует картинка 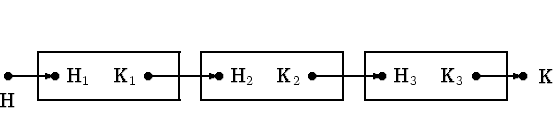$\begin{displaymath} { \setlength {\unitlength}{.032\textwidth} \thicklines ... ...(24,2){\circle*{.3}} \put(24,1){\makebox(2,2){К}}\end{picture}}\end{displaymath}$ Наконец, итерации соответствует картинка $\begin{displaymath} { \setlength {\unitlength}{.04\textwidth} \begin{picture} (... ...(6,5){\circle*{.3}} \put(6,4){\makebox(2,2){К}} %\end{picture}}\end{displaymath}$ $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 10.7.10. Дан источник. Построить конечный автомат, проверяющий, принадлежит ли входное слово соответствующему множеству (то есть можно ли прочесть это слово, идя из Н в К).

Решение. Состояниями автомата будут множества вершин источника. Именно, прочтя некоторое начало X входного слова, мы будем помнить множество всех вершин источника, в которые можно пройти из начальной, прочитав на пути слово X . $\scriptstyle\blacktriangleleft$

Оказывается, что регулярные выражения, автоматы и источники распознают одни и те же множества. Чтобы убедиться в этом, нам осталось решить такую задачу:

$\scriptstyle{\blacktriangleright}$ 10.7.11. Дан источник. Построить регулярное выражение, задающее то же множество, что и этот источник.

Решение. (Сообщено участниками просеминара по логике.) Пусть источник имеет вершины $1,\ldots,k$ . Будем считать, что 1 -- это начало, а k -- конец. Через D_i,j,s обозначим множество всех слов, которые можно прочесть на пути из i в j , если в качестве промежуточных пунктов разрешается использовать только вершины $1,\ldots,s$ . Согласно определению, источнику соответствует множество D_1,k,k .

Индукцией по s будем доказывать регулярность всех множеств D_i,j,s при всех i и j . При s=0 это очевидно (промежуточные вершины запрещены, поэтому каждое из множеств состоит только из букв).

Из чего состоит множество D_i,j,s+1 ? Отметим на пути моменты, в которых он заходит в (s+1) -ую вершину. При этом путь разбивается на части, каждая из которых уже не заходит в нее. Поэтому легко сообразить, что $\begin{displaymath} D_{i,j,s+1} = D_{i,j,s}\,\vert\, (D_{i,s+1,s}\;\;\; D_{s+1,s+1,s}{\hbox{\tt *}}\;\;\; D_{s+1,j,s})\end{displaymath}$ (вольность записи: мы используем для операций над множествами обозначения как для регулярных выражений). Остается воспользоваться предположением индукции. $\scriptstyle\blacktriangleleft$ $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 10.7.12. Где еще используется то же самое рассуждение?

Ответ. В алгоритме Флойда вычисления цены кратчайшего пути, см. главу 9. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 10.7.13. Доказать, что класс множеств, задаваемых регулярными выражениями, не изменился бы, если бы мы разрешили использовать не только объединение, но и отрицание (а следовательно, и пересечение -- оно выражается через объединение и отрицание).

Решение. Для автоматов переход к отрицанию очевиден. $\scriptstyle\blacktriangleleft$

Замечание. На практике важную роль играет число состояний автомата. Оказывается, что тут все не так просто, и переход от источника к автомату требует экспоненциального роста числа состояний. Подробное рассмотрение связанных с этим теоретических и практических вопросов -- дело особое (см. книгу Ахо, Ульмана и Сети о компиляторах).

pvv
1/8/1999