Повторения в образце --
источник проблем

Повторения в образце -- источник проблем


$\scriptstyle{\blacktriangleright}$ 10.2.1. Можно ли в предыдущих рассуждениях заменить слово abcd на произвольное слово?

Решение. Нет, и проблемы связаны с тем, что в образце могут быть повторяющиеся буквы. Пусть, например, мы ищем вхождения слова ababc. Вот появилась буква a, за ней идет b, за ней идет a, затем снова b. В этот момент мы с нетерпением ждем буквы c. Однако -- к нашему разочарованию -- вместо нее появляется другая буква, и наш образец ababc не обнаружен. Однако нас может ожидать утешительный приз: если вместо c появилась буква a, то не все потеряно: за ней могут последовать буквы b и c, и образец-таки будет найден.

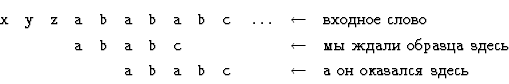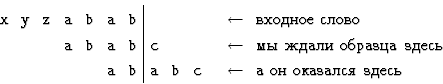Вот картинка, поясняющая сказанное: \begin{displaymath} \footnotesize \begin{tabular} {llllllllllllll} {\hbox{\tt x}... ...box{\tt c}}& &$\leftarrow$&а он оказался здесь\\ \end{tabular}\end{displaymath}Таким образом, к моменту \begin{displaymath} \footnotesize \begin{tabular} {lllllll\vert lllllll} {\hbox{... ...box{\tt c}}& &$\leftarrow$&а он оказался здесь\\ \end{tabular}\end{displaymath}есть два возможных положения образца, каждое из которых подлежит проверке. Тем не менее по-прежнему возможен конечный автомат, читающий входное слово буква за буквой и переходящий из состояния в состояние в зависимости от прочитанных букв.$\scriptstyle\blacktriangleleft$


$\scriptstyle{\blacktriangleright}$ 10.2.2. Указать состояния соответствующего автомата и таблицу перехода (новое состояние в зависимости от старого и читаемой буквы).

Решение. По-прежнему состояния будут соответствовать наибольшему началу образца, являющемуся концом прочитанной части слова. Их будет шесть: 0, 1 (a), 2 (ab), 3 (aba), 4 (abab), 5 (ababc). Таблица перехода: \begin{displaymath} \begin{tabular} {\vert l\vert l\vert l\vert} \hline Текуще... ... кроме {\hbox{\tt a}},{\hbox{\tt c}} & 0 \\ \hline\end{tabular}\end{displaymath}Для проверки посмотрим, к примеру, на вторую снизу строку. Если прочитанная часть кончалась на abab, а затем появилась буква a, то теперь прочитанная часть кончается на ababa. Наибольшее начало образца (ababc), являющееся ее концом -- это aba.$\scriptstyle\blacktriangleleft$

Философский вопрос: мы говорили, что трудность состоит в том, что есть несколько возможных положений образца, каждое из которых может оказаться истинным. Им соответствуют несколько начал образца, являющихся концами входного слова. Но конечный автомат помнит лишь самое длинное из них. Как же остальные?

Философский ответ. Дело в том, что самое длинное из них определяет все остальные -- это его концы, одновременно являющиеся его началами.

Не составляет труда для любого конкретного образца написать программу, осуществляющую поиск этого образца описанным способом. Однако хотелось бы написать программу, которая ищет произвольный образец в произвольном слове. Это можно делать в два этапа: сначала по образцу строится таблица переходов конечного автомата, а затем читается входное слово и состояние преобразуется в соответствии с этой таблицей. Подобный метод часто используется для более сложных задач поиска (см. далее), но для поиска подслова существует более простой и эффективный алгоритм, называемый алгоритмом Кнута-Морриса-Пратта.    (Ранее сходные идеи были предложены Ю.В. Матиясевичем)   Но прежде нам понадобятся некоторые вспомогательные утверждения.


pvv
1/8/1999