Рекурсивная обработка деревьев

Двоичным деревом называется картинка вроде такой: 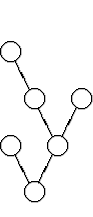$\begin{displaymath} \setlength {\unitlength}{7mm} \begin{picture} (5,8) \put(... ...1.4){\line(1,2){.6}} \put(3.2,3.4){\line(1,2){.6}}\end{picture}\end{displaymath}$ Нижняя вершина называется корнем. Из каждой вершины могут идти две линии: влево вверх и вправо вверх. Вершины, куда они ведут, называются левым и правым сыновьями исходной вершины. Вершина может иметь двух сыновей, а может иметь только одного сына (левого или правого). Она может и вовсе не иметь сыновей, и в этом случае называется листом.

Пусть x -- какая-то вершина двоичного дерева. Она сама вместе с сыновьями, внуками, правнуками и т. д. образует поддерево с корнем в x -- поддерево потомков x .

В следующих задачах мы предполагаем, что вершины дерева пронумерованы целыми положительными числами, причем номера всех вершин различны. Мы считаем, что номер корня хранится в переменной root. Мы считаем, что имеются два массива

        l,r: array [1..N] of integer

и левый и правый сын вершины с номером i имеют соответственно номера l[i] и r[i]. Если вершина с номером i не имеет левого (или правого) сына, то l[i] (соответственно r[i]) равно 0. (По традиции при записи программ мы используем вместо нуля константу nil, равную нулю.)

Здесь N -- достаточно большое натуральное число (номера всех вершин не превосходят N). Отметим, что номер вершины никак не связан с ее положением в дереве и что не все числа от 1 до N обязаны быть номерами вершин (и, следовательно, часть данных в массивах l и r -- это мусор).

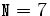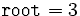$\scriptstyle{\blacktriangleright}$ 7.2.1. Пусть ${\hbox{\tt N}}=7$ , ${\hbox{\tt root}}=3$ , массивы l и r таковы:

$\begin{displaymath} \begin{tabular} {r\vert ccccccc} {\hbox{\tt i}}& 1& 2& 3& 4... ... 6& 0& 7\\ {\hbox{\tt r[i]}}& 0& 0& 5& 3& 2& 0& 7\end{tabular}\end{displaymath}$ Нарисовать соответствующее дерево.

Ответ:

$\begin{displaymath} \hskip500cm minus500cm \setlength {\unitlength}{7mm} \beg... ...ap{\kern.5em\hbox{\normalsize$\scriptstyle\blacktriangleleft$}}\end{displaymath}$

$\scriptstyle{\blacktriangleright}$ 7.2.2. Написать программу подсчета числа вершин в дереве.

Решение. Рассмотрим функцию n(x), равную числу вершин в поддереве с корнем в вершине номер x. Считаем, что 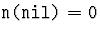${\hbox{\tt n(nil)}}={\hbox{\tt 0}}$ (полагая соответствующее поддерево пустым), и не заботимся о значениях nil(s) для чисел s, не являющихся номерами вершин. Рекурсивная программа для s такова:

     function n(x:integer):integer;
     begin
     | if x = nil then begin
     | | n:= 0;
     | end else begin
     | | n:= n(l[x]) + n(r[x]) + 1;
     | end;
     end;

(Число вершин в поддереве над вершиной x равно сумме чисел вершин над ее сыновьями плюс она сама.) Глубина рекурсии конечна, так как с каждым шагом высота соответствующего поддерева уменьшается. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 7.2.3. Написать программу подсчета числа листьев в дереве.

Ответ:

   function n (x:integer):integer;
   begin
   | if x = nil then begin
   | | n:= 0;
   | end else if (l[x]=nil) and (r[x]=nil) then begin {лист}
   | | n:= 1;
   | end else begin
   | | n:= n(l[x]) + n(r[x]);
   | end;
   end;`

$\scriptstyle{\blacktriangleright}$ 7.2.4. Написать программу подсчета высоты дерева (корень имеет высоту , его сыновья -- высоту 1 , внуки -- 2 и т. п.; высота дерева -- это максимум высот его вершин).

[Указание. Рекурсивно определяется функция 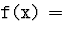${\hbox{\tt f(x)}} = {}$ высота поддерева с корнем в x.] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 7.2.5. Написать программу, которая по заданному n считает число всех вершин высоты n (в заданном дереве). $\scriptstyle\blacktriangleleft$

Вместо подсчета количества вершин того или иного рода можно просить напечатать список этих вершин (в том или ином порядке).

$\scriptstyle{\blacktriangleright}$ 7.2.6. Написать программу, которая печатает (по одному разу) все вершины дерева.

Решение. Процедура print_subtree(x) печатает все вершины поддерева с корнем в x по одному разу; главная программа содержит вызов print_subtree(root).

     procedure print_subtree (x:integer);
     begin
     | if x = nil then begin
     | | {ничего не делать}
     | end else begin
     | | writeln (x);
     | | print_subtree (l[x]);
     | | print_subtree (r[x]);
     | end;
     end;

Данная программа печатает сначала корень поддерева, затем поддерево над левым сыном, а затем над правым. Три строки в else-части могут быть переставлены 6 способами, и каждый из этих способов дает свой порядок печати вершин. $\scriptstyle\blacktriangleleft$

pvv
1/8/1999