Массивы

В следующих задачах переменные ${\hbox{\tt x}},{\hbox{\tt y}},{\hbox{\tt z}}$ предполагаются описанными как array[1..n] of integer (где n -- некоторое натуральное число, большее 0), если иное не оговорено явно.

$\scriptstyle{\blacktriangleright}$ 1.2.1. Заполнить массив x нулями. (Это означает, что нужно составить фрагмент программы, после выполнения которого все значения x[1]..x[n] равнялись бы нулю, независимо от начального значения переменной x.)

Решение:

          i := 0;
          {инвариант: первые i значений x[1]..x[i] равны 0}
          while i <> n do begin
          | i := i + 1;
          | {x[1]..x[i-1] = 0}
          | x[i] := 0;
          end;`

$\scriptstyle{\blacktriangleright}$ 1.2.2. Подсчитать количество нулей в массиве x. (Составить фрагмент программы, не меняющий значения x, после исполнения которого значение некоторой целой переменной k равнялось бы числу нулей среди компонент массива x.)

Решение:

          ...
          {инвариант: k = число нулей среди x[1]...x[i] }
          ...  `

$\scriptstyle{\blacktriangleright}$ 1.2.3. Не используя оператора присваивания для массивов, составить фрагмент программы, эквивалентный оператору x:=y.

Решение:

  i := 0;
  {инвариант: значение y не изменилось, x[l]=y[l] при l<=i}
  while i <> n do begin
  | i := i + 1;
  | x[i] := y[i];
  end;`

$\scriptstyle{\blacktriangleright}$ 1.2.4. Найти максимум из x[1]..x[n].

Решение:

          i := 1; max := x[1];
          {инвариант: max = максимум из x[1]..x[i]}
          while i <> n do begin
          | i := i + 1;
          | {max = максимум из x[1]..x[i-1]}
          | if x[i] > max then begin
          | | max := x[i];
          | end;
          end;`

$\scriptstyle{\blacktriangleright}$ 1.2.5. Дан массив x: array[1..n] of integer, причем ${\hbox{\tt x[1]}}\leqslant{\hbox{\tt x[2]}}\leqslant\ldots\leqslant{\hbox{\tt x[n]}}$ . Найти количество различных чисел среди элементов этого массива.

Решение. Вариант 1:

  i := 1; k := 1;
  {инвариант: k - количество различных среди x[1]..x[i]}
  while i <> n do begin
  | i := i + 1;
  | if x[i] <> x[i-1] then begin
  | | k := k + 1;
  | end;
  end;

Вариант 2. Искомое число на 1 больше количества тех чисел i из 1..n-1, для которых x[i] не равно x[i+1].

  k := 1;
  for i := 1 to n-1 do begin
  | if x[i]<> x[i+1] then begin
  | | k := k + 1;
  | end;
  end;`

$\scriptstyle{\blacktriangleright}$ 1.2.6 (Сообщил А.Л. Брудно.) Прямоугольное поле ${\hbox{\tt m}}\times{\hbox{\tt n}}$ разбито на ${\hbox{\tt mn}}$ квадратных клеток. Некоторые клетки покрашены в черный цвет. Известно, что все черные клетки могут быть разбиты на несколько непересекающихся и не имеющих общих вершин черных прямоугольников. Считая, что цвета клеток даны в виде массива типа $\begin{displaymath} {\hbox{\tt array [1..m] of array [1..n] of boolean;}}\end{displaymath}$ подсчитать число черных прямоугольников, о которых шла речь. Число действий должно быть порядка ${\hbox{\tt mn}}$ .

Решение. Число прямоугольников равно числу их левых верхних углов. Является ли клетка верхним углом, можно узнать, посмотрев на ее цвет, а также цвет верхнего и левого соседей. (Не забудьте, что их может не быть, если клетка с краю.) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.7. Дан массив x: array[1..n] of integer. Найти количество различных чисел среди элементов этого массива. (Число действий должно быть порядка ${\hbox{\tt n}}^2$ .) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.8. Та же задача, если требуется, чтобы количество действий было порядка ${\hbox{\tt n}}\,\log{\hbox{\tt n}}$ .

[Указание. Смотри главу 4 (Сортировка)] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.9. Та же задача, если известно, что все элементы массива -- числа от 1 до k и число действий должно быть порядка ${\hbox{\tt n}}+{\hbox{\tt k}}$ . $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.10. Дан массив x[1]..x[n] целых чисел. Не используя других массивов, переставить элементы массива в обратном порядке.

Решение. Числа x[i] и x[n+1-i] нужно поменять местами для всех i, для которых ${\hbox{\tt i}}<{\hbox{\tt n}}+{\hbox{\tt 1}}-{\hbox{\tt i}}$ ,то есть ${\hbox{\tt 2}}{\hbox{\tt i}} < {\hbox{\tt n}} + {\hbox{\tt 1}}$ $\Leftrightarrow$ ${\hbox{\tt 2}}{\hbox{\tt i}}\leqslant{\hbox{\tt n}}$ $\Leftrightarrow$ ${\hbox{\tt i}} \leqslant{\hbox{\tt n div 2}}$ :

  for i := 1 to n div 2 do begin
  | ...обменять x [i] и x [n+1-i];
  end;`

$\scriptstyle{\blacktriangleright}$ 1.2.11 (из книги Д. Гриса). Дан массив целых чисел
x[1]..x[m+n], рассматриваемый как соединение двух его отрезков: начала x[1]..x[m] длины m и конца x[m+1]..x[m+n] длины n. Не используя дополнительных массивов, переставить начало и конец. (Число действий порядка ${\hbox{\tt m}}+{\hbox{\tt n}}$ .)

Решение:

Вариант 1. Перевернем (расположим в обратном порядке) отдельно начало и конец массива, а затем перевернем весь массив как единое целое.

Вариант 2, А.Г. Кушниренко. Рассматривая массив записанным по кругу, видим, что требуемое действие -- поворот круга. Как известно, поворот есть композиция двух осевых симметрий.

Вариант 3. Рассмотрим более общую задачу -- обмен двух участков массива x[p+1]..x[q] и x[q+1]..x[r]. Предположим, что длина левого участка (назовем его A ) не больше длины правого (назовем его B ). Выделим в B начало той же длины, что и A , назовем его B₁ , а остаток B₂ . (Так что B=B₁+B₂ , если обозначать плюсом приписывание массивов друг к другу.) Нам надо из A+B₁+B₂ получить B₁+B₂+A . Меняя местами участки A и B₁ -- они имеют одинаковую длину, и сделать это легко,-- получаем B₁ + A + B₂ , и осталось поменять местами A и B₂ . Тем самым мы свели дело к перестановке двух отрезков меньшей длины. Итак, получаем такую схему программы:

 p := 0; q := m; r := m + n;
  {инвариант: осталось переставить x[p+1..q], x[q+1..r]}
  while (p <> q) and (q <> r) do begin
  | {оба участка непусты}
  | if (q - p) <= (r - q) then begin
  | | ..переставить x[p+1]..x[q] и x[q+1]..x[q+(q-p)]
  | | pnew := q; qnew := q + (q - p);
  | | p := pnew; q := qnew;
  | end else begin
  | | ..переставить x[q-(r-q)+1]..x[q] и x[q+1]..x[r]
  | | qnew := q - (r - q); rnew := q;
  | | q := qnew; r := rnew;
  | end;
  end;

Оценка времени работы: на очередном шаге оставшийся для обработки участок становится короче на длину A ; число действий при этом также пропорционально длине A . $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.12. Коэффициенты многочлена лежат в массиве $\begin{displaymath} {\hbox{\tt a:\ array[0..n]}}\ {\hbox{\tt of}}\ {\hbox{\tt integer}} \end{displaymath}$ (n -- натуральное число, степень многочлена). Вычислить значение этого многочлена в точке x, то есть ${\hbox{\tt a[n]}}\,{\hbox{\tt x}}^{\hbox{\tt n}}+\ldots+{\hbox{\tt a[1]}}\,{\hbox{\tt x}}+{\hbox{\tt a[0]}}$ .

Решение:

(Описываемый алгоритм называется схемой Горнера.)

  k := 0; y := a[n];
  {инвариант: 0 <= k <= n,
   y= a[n]*(x в степени k)+...+a[n-1]*(x в степени k-1)+...+
                     + a[n-k]*(x в степени 0)}
  while k<>n do begin
  | k := k + 1;
  | y := y * x + a [n-k];
  end;`

$\scriptstyle{\blacktriangleright}$ 1.2.13. (Для знакомых с основами анализа. Сообщил А.Г. Кушниренко) Дополнить алгоритм вычисления значения многочлена в заданной точке по схеме Горнера вычислением значения его производной в той же точке.

Решение. Добавление нового коэффициента соответствует переходу от многочлена P(x) к многочлену xP(x)+c . Его производная в точке x равна xP'(x) + P(x) . (Это решение обладает забавным свойством: не надо знать заранее степень многочлена. Если требовать выполнения этого условия, да еще просить вычислять только значение производной, не упоминая о самом многочлене, получается не такая уж простая задача.) $\scriptstyle\blacktriangleleft$

Общее утверждение о сложности вычисления производных таково:

$\scriptstyle{\blacktriangleright}$ 1.2.14. Дана программа вычисления значения некоторого многочлена $P(x_1,\ldots,x_n)$ , содержащая только команды присваивания. Их правые части -- выражения, содержащие сложение, умножение, константы, переменные $x_1,\ldots,x_n$ и ранее встречавшиеся (в левой части) переменные. Доказать, что существует программа того же типа, вычисляющая все n производных $\partial P/\partial x_1,\ldots, \partial P/\partial x_n$ ,причем общее число арифметических операций не более чем в C раз превосходит число арифметических операций в исходной программе. Константа C не зависит от n . (В. Баур, Ф. Штрассен)

[Указание. Можно считать, что каждая команда -- сложение двух чисел, умножение двух чисел или умножение на константу. Использовать индукцию по числу команд, применяя индуктивное предположение к программе, получающейся отбрасыванием первой команды.] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.15. В массивах $\begin{displaymath} {\hbox{\tt a:\ array[0..k]}}\ {\hbox{\tt of}}\ {\hbox{\tt in... ...x{\tt b:\ array[0..l]}}\ {\hbox{\tt of}}\ {\hbox{\tt integer}} \end{displaymath}$ хранятся коэффициенты двух многочленов степеней k и l. Поместить в массив c: array[0..m] of integer коэффициенты их произведения. (Числа ${\hbox{\tt k}},{\hbox{\tt l}},{\hbox{\tt m}}$ -- натуральные, ${\hbox{\tt m}}={\hbox{\tt k}}+{\hbox{\tt l}}$ ; элемент массива с индексом i содержит коэффициент при степени i.)

Решение:

          for i:=0 to m do begin
          | c[i]:=0;
          end;
          for i:=0 to k do begin
          | for j:=0 to l do begin
          | | c[i+j] := c[i+j] + a[i]*b[j];
          | end;
          end;`

$\scriptstyle{\blacktriangleright}$ 1.2.16. Предложенный выше алгоритм перемножения многочленов требует порядка n² действий для перемножения двух многочленов степени n . Придумать более эффективный (для больших n ) алгоритм, которому достаточно порядка $n^{\log 4/\log 3}$ действий.

[Указание. Представим себе, что надо перемножить два многочлена степени 2k . Их можно представить в виде $\begin{displaymath} A(x)\,x^k + B(x) \quad {\hbox{\tt и}} \quad C(x)\,x^k + D(x)\end{displaymath}$ Произведение их равно $\begin{displaymath} A(x)C(x)\,x^{2k} + (A(x)D(x)+B(x)C(x))\,x^k + B(x)D(x).\end{displaymath}$ Естественный способ вычисления AC , AD+BC , BD требует четырех умножений многочленов степени k , однако их количество можно сократить до трех с помощью такой хитрости: вычислить AC , BD и (A+B)(C+D) , а затем заметить, что AD+BC=(A+B)(C+D)-AC-BD .] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.17. Даны два возрастающих массива x: array[1..k] of integer и y: array[1..l] of integer. Найти количество общих элементов в этих массивах, то есть количество тех целых t, для которых ${\hbox{\tt t}} = {\hbox{\tt x[i]}} = {\hbox{\tt y[j]}}$ для некоторых i и j. (Число действий порядка ${\hbox{\tt k}}+{\hbox{\tt l}}$ .)

Решение:

  k1:=0; l1:=0; n:=0;
  {инвариант: 0<=k1<=k; 0<=l1<=l;
   искомый ответ = n + количество общих
   элементов в x[k1+1]...x[k] и y[l1+1]...y[l]}
  while (k1 <> k) and (l1 <> l) do begin
  | if x[k1+1] < y[l1+1] then begin
  | | k1 := k1 + 1;
  | end else if x[k1+1] > y[l1+1] then begin
  | | l1 := l1 + 1;
  | end else begin {x[k1+1] = y[l1+1]}
  | | k1 := k1 + 1;
  | | l1 := l1 + 1;
  | | n := n + 1;
  | end;
  end;
  {k1 = k или l1 = l, поэтому одно из множеств, упомянутых в
   инварианте, пусто, а n равно искомому ответу}`

Замечание. В третьей альтернативе достаточно было бы увеличивать одну из переменных k1, l1; вторая добавлена для симметрии.

$\scriptstyle{\blacktriangleright}$ 1.2.18. Решить предыдущую задачу, если известно лишь, что ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[k]}}$ и ${\hbox{\tt y[1]}}\leqslant\ldots\leqslant{\hbox{\tt y[l]}}$ (возрастание заменено неубыванием).

Решение. Условие возрастания было использовано в третьей альтернативе выбора: сдвинув k1 и l1 на 1, мы тем самым уменьшали на 1 количество общих элементов в ${\hbox{\tt x[k1+1]}}\ldots{\hbox{\tt x[k]}}$ и ${\hbox{\tt x[l1+1]}}\ldots{\hbox{\tt x[l]}}$ .Теперь это придется делать сложнее.

          ...
          end else begin {x[k1+1] = y[l1+1]}
          | t := x [k1+1];
          | while (k1<k) and (x[k1+1]=t) do begin
          | | k1 := k1 + 1;
          | end;
          | while (l1<l) and (x[l1+1]=t) do begin
          | | l1 := l1 + 1;
          | end;
          end;`

Замечание. Эта программа имеет дефект: при проверке условия $\begin{displaymath} {\hbox{\tt (l1<l) and (x[l1+1]=t)}}\end{displaymath}$ (или второго, аналогичного) при ложной первой скобке вторая окажется бессмысленной (индекс выйдет за границы массива) и возникнет ошибка. Некоторые версии паскаля, вычисляя A and B, сначала вычисляют A и при ложном A не вычисляют B. (Так ведет себя, например, система Turbo Pascal, 5.0 -- но не 3.0.) Тогда описанная ошибка не возникнет.

Но если мы не хотим полагаться на такое свойство используемой нами реализации паскаля (не предусмотренное его автором Н. Виртом), то можно поступить так. Введем дополнительную переменную b: boolean и напишем:

        if k1 < k  then b := (x[k1+1]=t)  else  b:=false;
        {b = (k1<k) and (x[k1+1] = t)}
        while  b  do  begin
        | k1:=k1+1;
        | if k1 < k then b := (x[k1+1]=t) else b:=false;
        end;

Можно также сделать иначе:

        end else begin {x[k1+1] = y[l1+1]}
        | if k1 + 1 = k then begin
        | | k1 := k1 + 1;
        | | n := n + 1;
        | end else if x[k1+1] = x [k1+2] then begin
        | | k1 := k1 + 1;
        | end else begin
        | | k1 := k1 + 1;
        | | n := n + 1;
        | end;
        end;

Так будет короче, хотя менее симметрично.

Наконец, можно увеличить размер массива в его описании, включив в него фиктивные элементы.

$\scriptstyle{\blacktriangleright}$ 1.2.19. Даны два неубывающих массива x: array[1..k] of integer и y: array[1..l] of integer. Найти число различных элементов среди ${\hbox{\tt x[1]}},\ldots,{\hbox{\tt x[k]}},{\hbox{\tt y[1]}},\ldots,{\hbox{\tt y[l]}}$ . (Число действий порядка ${\hbox{\tt k}}+{\hbox{\tt l}}$ .) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.20. Даны два массива ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[k]}}$ и ${\hbox{\tt y[1]}}\leqslant\ldots\leqslant{\hbox{\tt y[l]}}$ . << Соединить>> их в массив ${\hbox{\tt z[1]}}\leqslant\ldots\leqslant{\hbox{\tt z[m]}}$ ( ${\hbox{\tt m}}={\hbox{\tt k}}+{\hbox{\tt l}}$ ; каждый элемент должен входить в массив z столько раз, сколько раз он входит в общей сложности в массивы x и y). Число действий порядка m.

Решение:

 k1 := 0; l1 := 0;
 {инвариант: ответ получится, если к z[1]..z[k1+l1] добавить
  справа соединение массивов x[k1+1]..x[k] и y[l1+1]..y[l]}
 while (k1 <> k) or (l1 <> l) do begin
 | if k1 = k then begin
 | | {l1 < l}
 | | l1 := l1 + 1;
 | | z[k1+l1] := y[l1];
 | end else if l1 = l then begin
 | | {k1 < k}
 | | k1 := k1 + 1;
 | | z[k1+l1] := x[k1];
 | end else if x[k1+1] <= y[l1+1] then begin
 | | k1 := k1 + 1;
 | | z[k1+l1] := x[k1];
 | end else if x[k1+1] >= y[l1+1] then begin
 | | l1 := l1 + 1;
 | | z[k1+l1] := y[l1];
 | end else begin
 | | { такого не бывает }
 | end;
 end;
 {k1 = k, l1 = l, массивы соединены}

Этот процесс можно пояснить так. Пусть у нас есть две стопки карточек, отсортированных по алфавиту. Мы соединяем их в одну стопку, выбирая каждый раз ту из верхних карточек обеих стопок, которая идет раньше в алфавитном порядке. Если в одной стопке карточки кончились, берем их из другой стопки. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.21. Даны два массива ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[k]}}$ и ${\hbox{\tt y[1]}}\leqslant\ldots\leqslant{\hbox{\tt y[l]}}$ . Найти их << пересечение>>, то есть массив ${\hbox{\tt z[1]}}\leqslant\ldots\leqslant{\hbox{\tt z[m]}}$ , содержащий их общие элементы, причем кратность каждого элемента в массиве z равняется минимуму из его кратностей в массивах x и y. Число действий порядка ${\hbox{\tt k}}+{\hbox{\tt l}}$ . $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.22. Даны два массива ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[k]}}$ и ${\hbox{\tt y[1]}}\leqslant\ldots\leqslant{\hbox{\tt y[l]}}$ и число q. Найти сумму вида ${\hbox{\tt x[i]}}+{\hbox{\tt y[j]}}$ , наиболее близкую к числу q. (Число действий порядка k+l, дополнительная память -- фиксированное число целых переменных, сами массивы менять не разрешается.)

[Указание. Надо найти минимальное расстояние между элементами ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[k]}}$ и ${\hbox{\tt q}}-{\hbox{\tt y[l]}}\leqslant\ldots\leqslant{\hbox{\tt q}}-{\hbox{\tt y[1]}}$ , что нетрудно сделать в ходе их слияния в один (воображаемый) массив.] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.23. (из книги Д. Гриса) Некоторое число содержится в каждом из трех целочисленных неубывающих массивов ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[p]}}$ , ${\hbox{\tt y[1]}}\leqslant\ldots\leqslant{\hbox{\tt y[q]}}$ , ${\hbox{\tt z[1]}}\leqslant\ldots\leqslant{\hbox{\tt z[r]}}$ . Найти одно из таких чисел. Число действий должно быть порядка ${\hbox{\tt p}}+{\hbox{\tt q}}+{\hbox{\tt r}}$ .

Решение:

  p1:=1; q1=1; r1:=1;
  {инвариант: x[p1]..x[p], y[q1]..y[q], z[r1]..z[r]
   содержат общий элемент}
  while not ((x[p1]=y[q1]) and (y[q1]=z[r1])) do begin
  | if x[p1]<y[q1] then begin
  | | p1:=p1+1;
  | end else if y[q1]<z[r1] then begin
  | | q1:=q1+1;
  | end else if z[r1]<x[p1] then begin
  | | r1:=r1+1;
  | end else begin
  | | { так не бывает }
  | end;
  end;
  {x[p1] = y[q1] = z[r1]}
  writeln (x[p1]);`

$\scriptstyle{\blacktriangleright}$ 1.2.24. Та же задача, только заранее не известно, существует ли общий элемент в трех неубывающих массивах и требуется это выяснить (и найти один из общих элементов, если они есть). $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.25. Элементами массива a[1..n] являются неубывающие массивы [1..m] целых чисел: $\begin{displaymath} {\hbox{\tt a:\ array [1..n]\ of\ array [1..m]\ of\ integer;}}\end{displaymath}$ $\begin{displaymath} {\hbox{\tt a[1][1]}}\leqslant\ldots\leqslant{\hbox{\tt a[1][... ...hbox{\tt a[n][1]}}\leqslant\ldots\leqslant{\hbox{\tt a[n][m]}}.\end{displaymath}$ Известно, что существует число, входящее во все массивы a[i] (существует такое х, что для всякого i из 1..n найдется j из 1..m, для которого ${\hbox{\tt a[i][j]}}\mathbin={\hbox{\tt x}}$ ). Найти одно из таких чисел х.

Решение. Введем массив ${\hbox{\tt b[1]}}\ldots{\hbox{\tt b[n]}}$ , отмечающий начало << остающейся части>> массивов ${\hbox{\tt a[1]}},\ldots,{\hbox{\tt a[n]}}$ .

 for k:=1 to n do begin
 |  b[k]:=1;
 end;
 eq := true;
 for k := 2 to n do begin
 | eq := eq and (a[1][b[1]] = a[k][b[k]]);
 end;
 {инвариант: оставшиеся части пересекаются, т.е. существует
  такое х, что для всякого i из [1..n] найдется j из [1..m],
  не меньшее b[i], для которого a[i][j] = х;  eq <=> первые
  элементы оставшихся частей равны}
 while not eq do begin
 | s := 1; k := 1;
 | {a[s][b[s]] - минимальное среди a[1][b[1]]..a[k][b[k]]}
 | while k <> n do begin
 | | k := k + 1;
 | | if a[k][b[k]] < a[s][b[s]] then begin
 | | | s := k;
 | | end;
 | end;
 | {a[s][b[s]] - минимальное среди a[1][b[1]]..a[n][b[n]]}
 | b [s] := b [s] + 1;
 | for k := 2 to n do begin
 | | eq := eq and (a[1][b[1]] = a[k][b[k]]);
 | end;
 end;
 writeln (a[1][b[1]]);`

$\scriptstyle{\blacktriangleright}$ 1.2.26. Приведенное решение предыдущей задачи требует порядка ${\hbox{\tt m}}{\hbox{\tt n}}^2$ действий. Придумать способ с числом действий порядка mn.

[Указание. Придется пожертвовать симметрией и выбрать одну из строк за основную. Двигаясь по основной строке, поддерживаем такое соотношение: во всех остальных строках отмечен максимальный элемент, не превосходящий текущего элемента основной строки.] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.27. (Двоичный поиск) Дана последовательность ${\hbox{\tt x[1]}}\leqslant\ldots\leqslant{\hbox{\tt x[n]}}$ целых чисел и число a. Выяснить, содержится ли a в этой последовательности, то есть существует ли i из 1..n, для которого ${\hbox{\tt x[i]}}={\hbox{\tt a}}$ .(Количество действий порядка $\log {\hbox{\tt n}}$ .)

Решение. (Предполагаем, что ${\hbox{\tt n}}\gt{\hbox{\tt 0}}$ .)

  l := 1; r := n+1;
  {r > l, если a есть вообще, то есть и среди x[l]..x[r-1]}
  while r - l <> 1 do begin
  | m := l + (r-l) div 2 ;
  | {l < m < r }
  | if x[m] <= a then begin
  | | l := m;
  | end else begin {x[m] > a}
  | | r := m;
  | end;
  end;

(Обратите внимание, что и в случае ${\hbox{\tt x[m]}} = {\hbox{\tt a}}$ инвариант не нарушается.)

Каждый раз ${\hbox{\tt r}}-{\hbox{\tt l}}$ уменьшается примерно вдвое, откуда и вытекает требуемая оценка числа действий. $\scriptstyle\blacktriangleleft$

Замечание:

$\begin{displaymath} {\hbox{\tt l}} + {\hbox{\tt (r-l)}}\,{\hbox{\tt div}}\,{\hbo... ...hbox{\tt r}}+{\hbox{\tt l}})\,{\hbox{\tt div}}\,{\hbox{\tt 2}}.\end{displaymath}$

$\scriptstyle{\blacktriangleright}$ 1.2.28. (Из книги Д. Гриса) Дан массив x: array[1..n] of array[1..m] of integer, упорядоченный по строкам и по столбцам: $\begin{displaymath} {\hbox{\tt x[i][j]}} \leqslant{\hbox{\tt x[i][j+1]}},\end{displaymath}$ $\begin{displaymath} {\hbox{\tt x[i][j]}} \leqslant{\hbox{\tt x[i+1][j]}},\end{displaymath}$ и число a. Требуется выяснить, встречается ли a среди x[i][j].

Решение. Представляя себе массив a как матрицу (прямоугольник, заполненный числами), мы выберем прямоугольник, в котором только и может содержаться a, и будем его сужать. Прямоугольник этот будет содержать x[i][j] при ${\hbox{\tt 1}}\leqslant{\hbox{\tt i}}\leqslant{\hbox{\tt l}}$ и ${\hbox{\tt k}}\leqslant{\hbox{\tt j}}\leqslant{\hbox{\tt m}}$ .

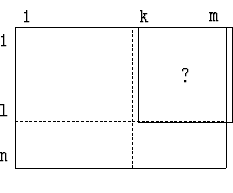$\begin{displaymath} \begin{picture} (11,8) \thinlines \put(1,1){\line(1,0){9... ...){{\hbox{\tt m}}}} \put(6,3){ \framebox (4,4){?}}\end{picture}\end{displaymath}$ (допускаются пустые прямоугольники при ${\hbox{\tt l}} = {\hbox{\tt 0}}$ и ${\hbox{\tt k}}={\hbox{\tt m}}+{\hbox{\tt 1}}$ ).

  l:=n; k:=1;
  {l>=0, k<=m+1, если a есть, то в описанном прямоугольнике}
  while (l > 0) and (k < m+1) and (x[l][k] <> a) do begin
  | if x[l][k] < a then begin
  | | k := k + 1; {левый столбец не содержит a, удаляем его}
  | end else begin {x[l][k] > a}
  | | l := l - 1; {нижняя строка не содержит a, удаляем ее}
  | end;
  end;
  {x[l][k] = a или прямоугольник пуст }
  answer:= (l > 0) and (k < m+1) ;`

Замечание. Здесь та же ошибка: x[l][k] может оказаться неопределенным. (Ее исправление предоставляется читателю.)

$\scriptstyle{\blacktriangleright}$ 1.2.29. (Московская олимпиада по программированию) Дан неубывающий массив положительных целых чисел ${\hbox{\tt a[1]}}\leqslant{\hbox{\tt a[2]}}\leqslant\ldots\leqslant{\hbox{\tt a[n]}}$ . Найти наименьшее целое положительное число, не представимое в виде суммы нескольких элементов этого массива (каждый элемент массива может быть использован не более одного раза). Число действий порядка n.

Решение. Пусть известно, что числа, представимые в виде суммы элементов ${\hbox{\tt a[1]}},\ldots,{\hbox{\tt a[k]}}$ , заполняют отрезок от 1 до некоторого N. Если ${\hbox{\tt a[k+1]}} \gt {\hbox{\tt N+1}}$ , то ${\hbox{\tt N+1}}$ и будет минимальным числом, не представимым в виде суммы элементов массива ${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[n]}}$ . Если же ${\hbox{\tt a[k+1]}}\leqslant{\hbox{\tt N+1}}$ , то числа, представимые в виде суммы элементов ${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[k+1]}}$ , заполняют отрезок от 1 до N+a[k+1].

  k := 0; N := 0;
  {инвариант: числа, представимые в виде суммы элементов
   массива a[1]..a[k], заполняют отрезок 1..N}
  while (k <> n) and (a[k+1] <= N+1) do begin
  | N := N + a[k+1];
  | k := k + 1;
  end;
  {(k = n) или (a[k+1] > N+1); в обоих случаях ответ N+1}
  writeln (N+1);

(Снова тот же дефект: в условии цикла при ложном первом условии второе не определено.) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.30. (Для знакомых с основами алгебры) В целочисленном массиве ${\hbox{\tt a[1]]}}\ldots{\hbox{\tt a[n]}}$ хранится перестановка чисел ${\hbox{\tt 1}}\ldots{\hbox{\tt n}}$ (каждое из чисел встречается по одному разу).

(а) Определить четность перестановки. (И в (а), и в (б) количество действий порядка n.)

(б) Не используя других массивов, заменить перестановку на обратную (если до работы программы ${\hbox{\tt a[i]}}={\hbox{\tt j}}$ , то после должно быть ${\hbox{\tt a[j]}}={\hbox{\tt i}}$ ).

[Указание. (а) Четность перестановки определяется количеством циклов. Чтобы отличать уже пройденные циклы, у их элементов можно, например, менять знак. (б) Обращение производим по циклам.] $\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.31. Дан массив a[1..n] и число b. Переставить числа в массиве таким образом, чтобы слева от некоторой границы стояли числа, меньшие или равные b, а справа от границы -- большие или равные b.

Решение:

        l:=0; r:=n;
        {инвариант: a[1]..a[l]<=b; a[r+1]..a[n]>=b}
        while l <> r do begin
        | if a[l+1] <= b then begin
        | | l:=l+1;
        | end else if a[r] >=b then begin
        | | r:=r-1;
        | end else begin {a[l+1]>b; a[r]<b}
        | | ..поменять a[l+1] и  a[r]
        | | l:=l+1; r:=r-1;
        | end;
        end;`

$\scriptstyle{\blacktriangleright}$ 1.2.32. Та же задача, но требуется, чтобы сначала шли элементы, меньшие b, затем равные b, а лишь затем большие b.

Решение. Теперь потребуются три границы: до первой будут идти элементы, меньшие b, от первой до второй -- равные b, затем неизвестно какие до третьей, а после третьей -- большие b. (Более симметричное решение использовало бы четыре границы, но вряд ли игра стоит свеч.) В качестве очередного рассматриваемого элемента берем элемент справа от средней границы.

     l:=0; m:=0; r:=n;
     {инвариант: a[1..l]<b; a[l+1..m]=b; a[r+1]..a[n]>b}
     while m <> r do begin
     | if a[m+1]=b then begin
     | | m:=m+1;
     | end else if a[m+1]>b then begin
     | | ..обменять a[m+1] и a[r]
     | | r:=r-1;
     | end else begin {a[m+1]<b}
     | | ..обменять a[m+1] и a[l+1]
     | | l:=l+1; m:=m+1;
     end;`

$\scriptstyle{\blacktriangleright}$ 1.2.33. (Вариант предыдущей задачи, названный в книге Дейкстры задачей о голландском флаге.) В массиве стоят числа 0, 1 и 2. Переставить их в порядке возрастания, если единственной разрешенной операцией (помимо чтения) над массивом является перестановка двух элементов. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.34. Дан массив a[1..n] и число ${\hbox{\tt m}}\leqslant{\hbox{\tt n}}$ . Для каждого участка из m стоящих рядом членов (таких участков, очевидно, ${\hbox{\tt n}}-{\hbox{\tt m}}+{\hbox{\tt 1}}$ ) вычислить его сумму. Общее число действий должно быть порядка n.

Решение. Переходя от участка к соседнему, мы добавляем один член, а другой вычитаем. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.35. Дана квадратная таблица a[1..n][1..n] и число ${\hbox{\tt m}}\leqslant{\hbox{\tt n}}$ . Для каждого квадрата ${\hbox{\tt m}}\times{\hbox{\tt m}}$ в этой таблице вычислить сумму стоящих в нем чисел. Общее число действий порядка ${\hbox{\tt n}}^2$ .

Решение. Сначала для каждого горизонтального прямоугольника размером ${\hbox{\tt m}}\times{\hbox{\tt 1}}$ вычисляем сумму стоящих в нем чисел. (При сдвиге такого прямоугольника по горизонтали на 1 нужно добавить одно число и одно вычесть.) Затем, используя эти суммы, вычисляем суммы в квадратах. (При сдвиге квадрата по вертикали добавляется полоска, а другая полоска убавляется.) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 1.2.36. В массиве ${\hbox{\tt a[1]}}\ldots{\hbox{\tt a[n]}}$ встречаются по одному разу все целые числа от 0 до n, кроме одного. Найти пропущенное число за время порядка n и с конечной дополнительной памятью.

[Указание. Сложить все числа в массиве.] $\blacktriangleleft$

Индуктивные функции

pvv
1/8/1999