![]() 1.1.1. Даны две целые переменные a, b.
Составить фрагмент программы, после исполнения которого значения
переменных поменялись бы местами (новое значение a равно
старому значению b и наоборот).
1.1.1. Даны две целые переменные a, b.
Составить фрагмент программы, после исполнения которого значения
переменных поменялись бы местами (новое значение a равно
старому значению b и наоборот).
t := a;
a := b;
b := t;
Попытка обойтись без дополнительной переменной, написав
a := b;
b := a;
не приводит к цели (безвозвратно утрачивается начальное значение
переменной a).
![]() 1.1.2. Решить предыдущую задачу, не используя
дополнительных переменных (и предполагая, что значениями целых
переменных могут быть произвольные целые числа).
1.1.2. Решить предыдущую задачу, не используя
дополнительных переменных (и предполагая, что значениями целых
переменных могут быть произвольные целые числа).
a := a + b; {a = a0 + b0, b = b0}
b := a - b; {a = a0 + b0, b = a0}
a := a - b; {a = b0, b = a0}`
![]() 1.1.3. Дано целое число а и натуральное (целое
неотрицательное) число n. Вычислить
1.1.3. Дано целое число а и натуральное (целое
неотрицательное) число n. Вычислить ![]() .Другими словами, необходимо составить
программу, при исполнении которой значения переменных а и
n не меняются, а значение некоторой другой переменной
(например, b) становится равным
.Другими словами, необходимо составить
программу, при исполнении которой значения переменных а и
n не меняются, а значение некоторой другой переменной
(например, b) становится равным ![]() .(При этом разрешается использовать и другие переменные.)
.(При этом разрешается использовать и другие переменные.)
k := 0; b := 1;
{b = a в степени k}
while k <> n do begin
| k := k + 1;
| b := b * a;
end;
Другое решение той же задачи:
k := n; b := 1;
{a в степени n = b * (a в степени k)}
while k <> 0 do begin
| k := k - 1;
| b := b * a;
end;`
![]() 1.1.4. Решить предыдущую задачу, если требуется, чтобы
число действий (выполняемых операторов присваивания) было
порядка
1.1.4. Решить предыдущую задачу, если требуется, чтобы
число действий (выполняемых операторов присваивания) было
порядка ![]() (то есть не превосходило бы
(то есть не превосходило бы
![]() для некоторой константы C ;
для некоторой константы C ; ![]() --
это степень, в которую нужно возвести 2 , чтобы получить
--
это степень, в которую нужно возвести 2 , чтобы получить ![]() ).
).
k := n; b := 1; c:=a;
{a в степени n = b * (c в степени k)}
while k <> 0 do begin
| if k mod 2 = 0 then begin
| | k:= k div 2;
| | c:= c*c;
| end else begin
| | k := k - 1;
| | b := b * c;
| end;
end;
Каждый второй раз (не реже) будет выполняться первый вариант
оператора выбора (если k нечетно, то после вычитания единицы
становится четным), так что за два цикла величина k уменьшается
по крайней мере вдвое.![]()
![]() 1.1.5. Даны натуральные числа а, b.
Вычислить произведение
1.1.5. Даны натуральные числа а, b.
Вычислить произведение ![]() , используя
в программе лишь операции +, -, =, <>.
, используя
в программе лишь операции +, -, =, <>.
k := 0; c := 0;
{инвариант: c = a * k}
while k <> b do begin
| k := k + 1;
| c := c + a;
end;
{c = a * k и k = b, следовательно, c = a * b}`
![]() 1.1.6. Даны натуральные числа а и b. Вычислить их сумму
1.1.6. Даны натуральные числа а и b. Вычислить их сумму
![]() . Использовать операторы присваивания лишь вида
. Использовать операторы присваивания лишь вида
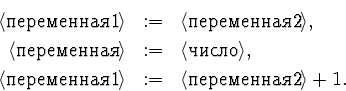
...
{инвариант: c = a + k}
...`
![]() 1.1.7. Дано натуральное (целое неотрицательное) число а
и целое положительное число d. Вычислить частное q и
остаток r при делении а на d, не используя операций
div и mod.
1.1.7. Дано натуральное (целое неотрицательное) число а
и целое положительное число d. Вычислить частное q и
остаток r при делении а на d, не используя операций
div и mod.
{a >= 0; d > 0}
r := a; q := 0;
{инвариант: a = q * d + r, 0 <= r}
while not (r < d) do begin
| {r >= d}
| r := r - d; {r >= 0}
| q := q + 1;
end;`
![]() 1.1.8. Дано натуральное
1.1.8. Дано натуральное ![]() , вычислить
, вычислить ![]() (
(![]() ,
, ![]() ).
).![]()
![]() 1.1.9. Последовательность Фибоначчи определяется так:
1.1.9. Последовательность Фибоначчи определяется так:
![]() ,
, ![]() ,
,![]() при
при ![]() . Дано
. Дано ![]() , вычислить
, вычислить ![]() .
.![]()
![]() 1.1.10. Та же задача, если требуется, чтобы число операций было
пропорционально
1.1.10. Та же задача, если требуется, чтобы число операций было
пропорционально ![]() . (Переменные должны быть
целочисленными.)
. (Переменные должны быть
целочисленными.)
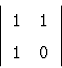 -- так что задача сводится к возведению матрицы в степень
-- так что задача сводится к возведению матрицы в степень
![]() 1.1.11. Дано натуральное n, вычислить
1.1.11. Дано натуральное n, вычислить
![]()
![]() 1.1.12. То же, если требуется, чтобы количество операций
(выполненных команд присваивания) было бы порядка
1.1.12. То же, если требуется, чтобы количество операций
(выполненных команд присваивания) было бы порядка ![]() (не более
(не более ![]() для
некоторой константы C ).
для
некоторой константы C ).
![]() 1.1.13. Даны два натуральных числа a и b, не равные нулю
одновременно. Вычислить НОД(a,b) -- наибольший общий
делитель а и b.
1.1.13. Даны два натуральных числа a и b, не равные нулю
одновременно. Вычислить НОД(a,b) -- наибольший общий
делитель а и b.
if a > b then begin
| k := a;
end else begin
| k := b;
end;
{k = max (a,b)}
{инвариант: никакое число, большее k, не является
общим делителем}
while not ((a mod k = 0) and (b mod k = 0)) do begin
| k := k - 1;
end;
{k - общий делитель, большие - нет}
Вариант 2 -- алгоритм Евклида:
Будем считать, что
НОД(0,0)=0. Тогда НОД(a,b) =
НОД(a-b,b) = НОД(a,b-a); НОД(a,0) = НОД(0,a) =
a для всех ![]() .
.
m := a; n := b;
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0 }
while not ((m=0) or (n=0)) do begin
| if m >= n then begin
| | m := m - n;
| end else begin
| | n := n - m;
| end;
end;
{m = 0 или n = 0}
if m = 0 then begin
| k := n;
end else begin {n = 0}
| k := m;
end;`
![]() 1.1.14. Написать модифицированный вариант алгоритма Евклида,
использующий соотношения
1.1.14. Написать модифицированный вариант алгоритма Евклида,
использующий соотношения
![]() 1.1.15. Даны натуральные a и b, не равные 0 одновременно.
Найти d = НОД(a,b) и такие целые x и y, что
1.1.15. Даны натуральные a и b, не равные 0 одновременно.
Найти d = НОД(a,b) и такие целые x и y, что
![]() .
.
m:=a; n:=b; p := 1; q := 0; r := 0; s := 1;
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0
m = p*a + q*b; n = r*a + s*b.}
while not ((m=0) or (n=0)) do begin
| if m >= n then begin
| | m := m - n; p := p - r; q := q - s;
| end else begin
| | n := n - m; r := r - p; s := s - q;
| end;
end;
if m = 0 then begin
| k :=n; x := r; y := s;
end else begin
| k := m; x := p; y := q;
end;`
![]() 1.1.16. Решить предыдущую задачу, используя в алгоритме Евклида
деление с остатком.
1.1.16. Решить предыдущую задачу, используя в алгоритме Евклида
деление с остатком.![]()
![]() 1.1.17. (Э. Дейкстра) Добавим в алгоритм Евклида дополнительные
переменные u, v, z:
1.1.17. (Э. Дейкстра) Добавим в алгоритм Евклида дополнительные
переменные u, v, z:
m := a; n := b; u := b; v := a;
{инвариант: НОД (a,b) = НОД (m,n); m,n >= 0 }
while not ((m=0) or (n=0)) do begin
| if m >= n then begin
| | m := m - n; v := v + u;
| end else begin
| | n := n - m; u := u + v;
| end;
end;
if m = 0 then begin
| z:= v;
end else begin {n=0}
| z:= u;
end;
Доказать, что после исполнения алгоритма значение
z равно удвоенному
наименьшему общему кратному чисел a, b:
![]() 1.1.18. Написать вариант алгоритма Евклида,
использующий соотношения
1.1.18. Написать вариант алгоритма Евклида,
использующий соотношения
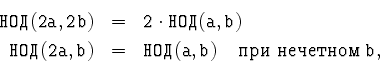 не включающий деления с остатком, а использующий лишь деление на 2 и
проверку четности. (Число действий должно быть порядка
не включающий деления с остатком, а использующий лишь деление на 2 и
проверку четности. (Число действий должно быть порядка ![]() для
исходных данных, не превосходящих k.)
для
исходных данных, не превосходящих k.)
m:= a; n:=b; d:=1;
{НОД(a,b) = d * НОД(m,n)}
while not ((m=0) or (n=0)) do begin
| if (m mod 2 = 0) and (n mod 2 = 0) then begin
| | d:= d*2; m:= m div 2; n:= n div 2;
| end else if (m mod 2 = 0) and (n mod 2 = 1) then begin
| | m:= m div 2;
| end else if(m mod 2 = 1) and (n mod 2 = 0) then begin
| | n:= n div 2;
| end else if(m mod 2=1)and(n mod 2=1)and(m>=n)then begin
| | m:= m-n;
| end else if(m mod 2=1)and(n mod 2=1)and(m<=n)then begin
| | n:= n-m;
| end;
end;
{m=0 => ответ=d*n; n=0 => ответ=d*m}
Оценка числа действий: каждое второе действие делит хотя бы одно
из чисел m и n пополам.
![]() 1.1.19. Дополнить алгоритм предыдущей задачи поиском x и y,
для которых
1.1.19. Дополнить алгоритм предыдущей задачи поиском x и y,
для которых ![]() .
.
Теперь попытаемся, как и раньше, хранить такие числа
![]() , что
, что
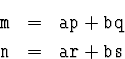 Проблема в том, что при делении, скажем, m на 2 надо
разделить p и q на 2, и они перестанут быть целыми
(а станут двоично-рациональными). Двоично-рациональное число
естественно хранить в виде пары
Проблема в том, что при делении, скажем, m на 2 надо
разделить p и q на 2, и они перестанут быть целыми
(а станут двоично-рациональными). Двоично-рациональное число
естественно хранить в виде пары ![]() числитель, показатель степени
двойки в знаменателе
числитель, показатель степени
двойки в знаменателе![]() . В итоге мы получаем d в виде
комбинации a и b с двоично-рациональными коэффициентами.
Иными словами, мы имеем
. В итоге мы получаем d в виде
комбинации a и b с двоично-рациональными коэффициентами.
Иными словами, мы имеем
![]() для некоторых целых
для некоторых целых ![]() и натурального
и натурального ![]() . Что
делать, если
. Что
делать, если ![]() ? Если x и y четны, то на 2
можно сократить. Если это не так, положение можно исправить
преобразованием
? Если x и y четны, то на 2
можно сократить. Если это не так, положение можно исправить
преобразованием
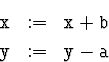 (оно не меняет
(оно не меняет ![]() ). Убедимся в этом.
Напомним, что мы считаем, что одно из чисел a и b
нечетно. Пусть это будет a. Если при этом y четно, то и
x должно быть четным (иначе
). Убедимся в этом.
Напомним, что мы считаем, что одно из чисел a и b
нечетно. Пусть это будет a. Если при этом y четно, то и
x должно быть четным (иначе ![]() будет
нечетным). А при нечетном y вычитание из него нечетного
a делает y четным.
будет
нечетным). А при нечетном y вычитание из него нечетного
a делает y четным.![]()
![]() 1.1.20. Составить программу, печатающую квадраты всех натуральных
чисел от 0 до заданного натурального n.
1.1.20. Составить программу, печатающую квадраты всех натуральных
чисел от 0 до заданного натурального n.
k:=0;
writeln (k*k);
{инвариант: k<=n, напечатаны все
квадраты до k включительно}
while not (k=n) do begin
| k:=k+1;
| writeln (k*k);
end;`
![]() 1.1.21. Та же задача, но разрешается использовать из арифметических
операций лишь сложение и вычитание, причем общее число действий
должно быть порядка n.
1.1.21. Та же задача, но разрешается использовать из арифметических
операций лишь сложение и вычитание, причем общее число действий
должно быть порядка n.
k_square (square -- квадрат),
связанную с k соотношением
k := 0; k_square := 0;
writeln (k_square);
while not (k = n) do begin
| k := k + 1;
| {k_square = (k-1) * (k-1) = k*k - 2*k + 1}
| k_square := k_square + k + k - 1;
| writeln (k_square);
end;`
Замечание. Можно обойтись без вычитания с помощью такой хитрости:
while not (k = n) do begin
| k_square := k_square + k;
| {k_square = k*k + k}
| k := k + 1;
| {k_square = (k-1)*(k-1)+(k-1)=k*k-k}
| k_square := k_square + k;
end;
![]() 1.1.22. Составить программу, печатающую разложение на простые
множители заданного натурального числа
1.1.22. Составить программу, печатающую разложение на простые
множители заданного натурального числа ![]() (другими
словами, требуется печатать только простые числа и произведение
напечатанных чисел должно быть равно n; если
(другими
словами, требуется печатать только простые числа и произведение
напечатанных чисел должно быть равно n; если ![]() , печатать ничего не надо).
, печатать ничего не надо).
k := n;
{инвариант: произведение напечатанных чисел и k равно
n, напечатаны только простые числа}
while not (k = 1) do begin
| l := 2;
| {инвариант: k не имеет делителей в интервале (1,l)}
| while k mod l <> 0 do begin
| | l := l + 1;
| end;
| {l - наименьший делитель k, больший 1, следовательно,
| простой}
| writeln (l);
| k:=k div l;
end;
Вариант 2:
k := n; l := 2;
{произведение k и напечатанных чисел равно n; напеча-
танные числа просты; k не имеет делителей, меньших l}
while not (k = 1) do begin
| if k mod l = 0 then begin
| | {k делится на l и не имеет делителей,
| | меньших l, значит, l просто}
| | k := k div l;
| | writeln (l);
| end else begin
| | { k не делится на l }
| | l := l+1;
| end;
end;`
![]() 1.1.23. Составить программу решения предыдущей задачи, использующую
тот факт, что составное число имеет делитель, не превосходящий
квадратного корня из этого числа.
1.1.23. Составить программу решения предыдущей задачи, использующую
тот факт, что составное число имеет делитель, не превосходящий
квадратного корня из этого числа.
if l*l > k then begin
| l:=k;
end else begin
| l:=l+1;
end;`
![]() 1.1.24. Проверить, является ли заданное натуральное число
1.1.24. Проверить, является ли заданное натуральное число
![]() простым.
простым. ![]()
![]() 1.1.25. (Для знакомых с основами алгебры) Дано целое гауссово число
1.1.25. (Для знакомых с основами алгебры) Дано целое гауссово число
![]() (принадлежащее
(принадлежащее ![]() ). (a) Проверить,
является ли оно простым (в
). (a) Проверить,
является ли оно простым (в ![]() ); (б) напечатать его
разложение на простые (в
); (б) напечатать его
разложение на простые (в ![]() ) множители.
) множители. ![]()
![]() 1.1.26. Разрешим применять команды write(i) лишь при
1.1.26. Разрешим применять команды write(i) лишь при
![]() . Составить программу,
печатающую десятичную запись заданного натурального числа
. Составить программу,
печатающую десятичную запись заданного натурального числа
![]() . (Случай
. (Случай ![]() явился бы некоторым
исключением, так как обычно нули в начале числа не печатаются, а
для
явился бы некоторым
исключением, так как обычно нули в начале числа не печатаются, а
для ![]() -- печатаются.)
-- печатаются.)
base:=1;
{base - степень 10, не превосходящая n}
while 10 * base <= n do begin
| base:= base * 10;
end;
{base - максимальная степень 10, не превосходящая n}
k:=n;
{инвариант: осталось напечатать k с тем же числом
знаков, что в base; base = 100..00}
while base <> 1 do begin
| write(k div base);
| k:= k mod base;
| base:= base div 10;
end;
{base=1; осталось напечатать однозначное число k}
write(k);
(Типичная ошибка при решении этой задачи: неправильно
обрабатываются числа с нулями посередине. Приведенный инвариант
допускает случай, когда
![]() 1.1.27. То же самое, но надо напечатать десятичную запись в
обратном порядке. (Для
1.1.27. То же самое, но надо напечатать десятичную запись в
обратном порядке. (Для ![]() надо напечатать 371.)
надо напечатать 371.)
k:= n;
{инвариант: осталось напечатать k в обратном порядке}
while k <> 0 do begin
| write (k mod 10);
| k:= k div 10;
end;`
![]() 1.1.28. Дано натуральное n. Подсчитать количество решений
неравенства
1.1.28. Дано натуральное n. Подсчитать количество решений
неравенства ![]() в натуральных
(неотрицательных целых) числах, не используя действий с
вещественными числами.
в натуральных
(неотрицательных целых) числах, не используя действий с
вещественными числами.
k := 0; s := 0;
{инвариант: s = количество решений неравенства
x*x + y*y < n c x < k}
while k*k < n do begin
| ...
| {t = число решений неравенства k*k + y*y < n
| с y>=0 (при данном k) }
| k := k + 1;
| s := s + t;
end;
{k*k >= n, поэтому s = количество всех решений
неравенства}
Здесь ... -- пока еще не написанный кусок программы, который будет таким:
l := 0; t := 0;
{инвариант: t = число решений
неравенства k*k + y*y < n c 0<=y<l }
while k*k + l*l < n do begin
| l := l + 1;
| t := t + 1;
end;
{k*k + l*l >= n, поэтому t = число
всех решений неравенства k*k + y*y < n}`
![]() 1.1.29. Та же задача, но количество операций должно быть порядка
1.1.29. Та же задача, но количество операций должно быть порядка
![]() . (В предыдущем решении, как можно подсчитать,
порядка n операций.)
. (В предыдущем решении, как можно подсчитать,
порядка n операций.)
 Идея решения состоит в том, чтобы << двигаться вдоль его
границы>>, спускаясь по верхнему его краю, как по лестнице.
Координаты движущейся точки обозначим <k,l>. Введем еще одну
переменную s и будем поддерживать истинность такого условия:
Идея решения состоит в том, чтобы << двигаться вдоль его
границы>>, спускаясь по верхнему его краю, как по лестнице.
Координаты движущейся точки обозначим <k,l>. Введем еще одну
переменную s и будем поддерживать истинность такого условия:
Формально:<k,l> находится сразу над k-ым столбцом;
s -- число точек в предыдущих столбцах.
k := 0; l := 0;
while <0,l> принадлежит X do begin
| l := l + 1;
end;
{k = 0, l - минимальное среди тех l >= 0,
для которых <k,l> не принадлежит X }
s := 0;
{инвариант: И}
while not (l = 0) do begin
| s := s + l;
| {s - число точек в столбцах до k-го включительно}
| k := k + 1;
| {точка <k,l> лежит вне X, но, возможно, ее надо сдвинуть
| вниз, чтобы восстановить И }
| while (l <> 0) and (<k, l-1> не принадлежит X) do begin
| | l := l - 1;
| end;
end;
{И, l = 0, поэтому k-ый столбец и все следующие пусты, а
s равно искомому числу}
Оценка числа действий очевидна: сначала мы движемся вверх не
более чем на
![]() 1.1.30. Даны натуральные числа n и k,
1.1.30. Даны натуральные числа n и k, ![]() .Напечатать k десятичных знаков числа
.Напечатать k десятичных знаков числа ![]() . (При
наличии двух десятичных разложений выбирается то из них, которое
не содержит девятки в периоде.) Программа должна использовать
только целые переменные.
. (При
наличии двух десятичных разложений выбирается то из них, которое
не содержит девятки в периоде.) Программа должна использовать
только целые переменные.
l := 0; r := 1;
{инв.: напечатано l разрядов 1/n, осталось напечатать
k - l разрядов дроби r/n}
while l <> k do begin
| write ( (10 * r) div n);
| r := (10 * r) mod n;
| l := l + 1;
end;`
![]() 1.1.31. Дано натуральное число
1.1.31. Дано натуральное число ![]() . Определить длину
периода десятичной записи дроби
. Определить длину
периода десятичной записи дроби ![]() .
.
l := 0; r := 1;
{инвариант: r/n = результат отбрасывания l знаков в 1/n}
while l <> n+1 do begin
| r := (10 * r) mod n;
| l := l + 1;
end;
c := r;
{c = (n+1)-ый член последовательности остатков}
r := (10 * r) mod n;
k := 1;
{r = (n+k+1)-ый член последовательности остатков}
while r <> c do begin
| r := (10 * r) mod n;
| k := k + 1;
end;`
![]() 1.1.32 (сообщил Ю.В. Матиясевич ).
Дана функция
1.1.32 (сообщил Ю.В. Матиясевич ).
Дана функция
![]() Найти период
последовательности
Найти период
последовательности ![]() ,
, ![]() ,
, ![]() .Количество действий
должно быть пропорционально периоду (который может быть
существенно меньше N).
.Количество действий
должно быть пропорционально периоду (который может быть
существенно меньше N).
{Обозначение: f[n,1]=f(f(...f(1)...)) (n раз)}
k:=1; a:=f(1); b:=f(f(1));
{a=f[k,1]; b=f[2k,1]}
while a <> b do begin
| k:=k+1; a:=f(a); b:=f(f(b));
end;
{a=f[k,1]=f[2k,1]; f[k,1] входит в периодическую часть
l:=1; b:=f(a);
{b=f[k+l,1]; f[k,1],...,f[k+l-1,1] различны}
while a <> b do begin
| l:=l+1; b:=f(b);
end;
{период равен l}`
![]() 1.1.33. (Э. Дейкстра). Функция f с натуральными аргументами
и значениями определена так:
1.1.33. (Э. Дейкстра). Функция f с натуральными аргументами
и значениями определена так: ![]() ,
,![]() ,
, ![]() ,
,![]() .Составить программу вычисления
.Составить программу вычисления ![]() по заданному
n, требующую порядка
по заданному
n, требующую порядка ![]() операций.
операций.
k := n; a := 1; b := 0;
{инвариант: 0 <= k, f (n) = a * f(k) + b * f (k+1)}
while k <> 0 do begin
| if k mod 2 = 0 then begin
| | l := k div 2;
| | {k=2l, f(k)=f(l), f(k+1) = f(2l+1) = f(l) + f(l+1),
| | f (n) = a*f(k) + b*f(k+1) = (a+b)*f(l) + b*f(l+1)}
| | a := a + b; k := l;
| end else begin
| | l := k div 2;
| | {k = 2l + 1, f(k) = f(l) + f(l+1),
| | f(k+1) = f(2l+2) = f(l+1),
| | f(n) = a*f(k) + b*f(k+1) = a*f(l) + (a+b)*f(l+1)}
| | b := a + b; k := l;
| end;
end;
{k = 0, f(n) = a * f(0) + b * f(1) = b, что и требовалось}`
![]() 1.1.34. То же, если
1.1.34. То же, если ![]() ,
,![]() ,
, ![]() ,
,![]() при
при ![]() .
.
![]() 1.1.35. Даны натуральные числа а и b, причем
1.1.35. Даны натуральные числа а и b, причем ![]() .Найти частное и остаток при делении a на b, оперируя лишь с
целыми числами и не используя операции div и mod, за
исключением деления на 2 четных чисел; число шагов не должно
превосходить
.Найти частное и остаток при делении a на b, оперируя лишь с
целыми числами и не используя операции div и mod, за
исключением деления на 2 четных чисел; число шагов не должно
превосходить ![]() для некоторых констант C1, C2 .
для некоторых констант C1, C2 .
b1 := b;
while b1 <= a do begin
| b1 := b1 * 2;
end;
{b1 > a, b1 = b * (некоторая степень 2)}
q:=0; r:=a;
{инвариант: q, r - частное и остаток при делении a на b1,
b1 = b * (некоторая степень 2)}
while b1 <> b do begin
| b1 := b1 div 2 ; q := q * 2;
| { a = b1 * q + r, 0 <= r, r < 2 * b1}
| if r >= b1 then begin
| | r := r - b1;
| | q := q + 1;
| end;
end;
{q, r - частное и остаток при делении a на b}`