Алгоритмы порядка

4.2.1. Предложить алгоритм сортировки, число действий которого было бы порядка , то есть не превосходило бы для некоторого C и для всех n .

Пусть k -- положительное целое число. Разобьем массив на отрезки длины k. (Первый -- , затем и так далее.) Последний отрезок будет неполным, если n не делится на k. Назовем массив k-упорядоченным, если каждый из этих отрезков в отдельности упорядочен. Любой массив 1-упорядочен. Если массив k-упорядочен и , то он упорядочен.

Мы опишем, как преобразовать k-упорядоченный массив в 2k-упорядоченный (из тех же элементов). С помощью этого преобразования алгоритм записывается так:

 k:=1;
 {массив x является k-упорядоченным}
 while k < n do begin
 | ..преобразовать k-упорядоченный массив в 2k-упорядоченный;
 | k := 2 * k;
 end;

Требуемое преобразование состоит в том,что мы многократно << сливаем>> два упорядоченных отрезка длины не больше k в один упорядоченный отрезок. Пусть процедура при сливает отрезки и в упорядоченный отрезок (не затрагивая других частей массива x).

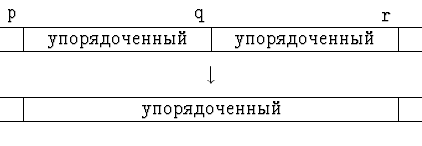Тогда преобразование k-упорядоченного массива в 2k-упорядоченный осуществляется так:

  t:=0;
  {t кратно 2k или t = n, x[1]..x[t] является
   2k-упорядоченным; остаток массива x не изменился}
  while t + k < n do begin
  | p := t;
  | q := t+k;
  | ...r := min (t+2*k, n); {min(a,b) - минимум из a и b}
  | слияние (p,q,r);
  | t := r;
  end;

        b[s0+1]:=x[p0+1];
        p0:=p0+1;
        s0:=s0+1;

        b[s0+1]:=x[q0+1];
        q0:=q0+1;
        s0:=s0+1;

(2) второй отрезок кончился () или не кончился, но элемент в нем не меньше очередного элемента первого отрезка  [) и ()].

Аналогично для второго действия. Итак, получаем

  p0 := p; q0 := q; s0 := p;
  while (p0 <> q) or (q0 <> r) do begin
  | if (p0 < q) and ((q0 = r) or ((q0 < r) and
  | |                (x[p0+1] <= x[q0+1]))) then begin
  | | b [s0+1] := x [p0+1];
  | | p0 := p0+1;
  | | s0 := s0+1;
  | end else begin
  | | {(q0 < r) and ((p0 = q) or ((p0<q) and
  | |   (x[p0+1] >= x[q0+1])))}
  | | b [s0+1] := x [q0+1];
  | | q0 := q0 + 1;
  | | s0 := s0 + 1;
  | end;
  end;

Остается лишь переписать результат слияния обратно в массив x.

Программа имеет привычный дефект: обращение к несуществующим элементам массива при вычислении булевских выражений. 

Нарисуем << полное двоичное дерево>> -- картинку, в    которой снизу один кружок, из него выходят стрелки в два других, из каждого -- в два других и так далее:

Будем говорить, что стрелки ведут << от отцов к сыновьям>>: у каждого кружка два сына и один отец (если кружок не в самом верху или низу). Предположим для простоты, что количество подлежащих сортировке чисел есть степень двойки, и они могут заполнить один из рядов целиком. Запишем их туда. Затем заполним часть дерева под ними по правилу: Тем самым в корне дерева (нижнем кружке) будет записано минимальное число во всем массиве.

Изымем из сортируемого массива минимальный элемент. Для этого его надо вначале найти. Это можно сделать, идя от корня: от отца переходим к тому сыну, где записано то же число. Изъяв минимальный элемент, заменим его символом и скорректируем более низкие ярусы (для этого надо снова пройти путь к корню). При этом считаем, что .Тогда в корне появится второй по величине элемент, мы изымаем его, заменяя бесконечностью и корректируя дерево. Так постепенно мы изымем все элементы в порядке возрастания, пока в корне не останется бесконечность.

При записи этого алгоритма полезно нумеровать кружки числами -- при этом сыновьями кружка номер n являются кружки 2n и . Подробное изложение этого алгоритма мы опустим, поскольку мы изложим более эффективный вариант, не требующий дополнительной памяти, кроме конечного числа переменных (в дополнение к сортируемому массиву).

Мы будем записывать сортируемые числа во всех вершинах дерева, а не только на верхнем уровне. Пусть -- массив, подлежащий сортировке. Вершинами дерева будут числа от 1 до n; о числе x[i] мы будем говорить как о числе, стоящем в вершине i. В процессе сортировки количество вершин дерева будет сокращаться. Число вершин текущего дерева будем хранить в переменной k. Таким образом, в процессе работы алгоритма массив делится на две части: в хранятся числа на дереве, а в хранится уже отсортированная в порядке возрастания часть массива -- элементы, уже занявшие свое законное место.

На каждом шаге алгоритм будет изымать максимальный элемент дерева и помещать его в отсортированную часть, на освободившееся в результате сокращения дерева место.

Договоримся о терминологии. Вершинами дерева считаются числа от 1 до текущего значения переменной k. У каждой вершины s могут быть сыновья 2s и 2s+1. Если оба этих числа больше k, то сыновей нет; такая вершина называется листом. Если , то вершина s имеет ровно одного сына (2s).

Для каждого s из рассмотрим << поддерево>> с корнем в s: оно содержит вершину s и всех ее потомков (сыновей, внуков и так далее -- до тех пор, пока мы не выйдем из отрезка ). Вершину s будем называть регулярной, если стоящее в ней число -- максимальный элемент s-поддерева; s-поддерево назовем регулярным, если все его вершины регулярны. (В частности, любой лист образует регулярное одноэлементное поддерево.)

Схема алгоритма такова:

 k:= n
 ... Сделать 1-поддерево регулярным;
 {x[1],..,x[k] <= x[k+1] <=..<= x[n]; 1-поддерево регулярно,
  в частности, x[1] - максимальный элемент среди x[1]..x[k]}
 while k <> 1 do begin
 | ... обменять местами x[1] и x[k];
 | k := k - 1;
 | {x[1]..x[k-1] <= x[k] <=...<= x[n]; 1-поддерево регу-
 |   лярно везде, кроме, возможно, самого корня }
 | ... восстановить регулярность 1-поддерева всюду
 end;

  {s-поддерево регулярно везде, кроме, возможно, корня}
  t := s;
  {s-поддерево регулярно везде, кроме, возможно, вершины t}
  while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or
  |     ((2*t <= k) and (x[2*t] > x[t])) do begin
  | if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin
  | | ... обменять x[t] и x[2*t+1];
  | | t := 2*t + 1;
  | end else begin
  | | ... обменять x[t] и x[2*t];
  | | t := 2*t;
  | end;
  end;

Чтобы убедиться в правильности этой процедуры, посмотрим на нее повнимательнее. Пусть в s-поддереве все вершины, кроме разве что вершины t, регулярны. Рассмотрим сыновей вершины t. Они регулярны, и потому содержат наибольшие числа в своих поддеревьях. Таким образом, на роль наибольшего числа в t-поддереве могут претендовать число в самой вершине t и числа в ее сыновьях. (В первом случае вершина t регулярна, и все в порядке.) В этих терминах цикл можно записать так:

while наибольшее число не в t, а в одном из сыновей do begin
| if оно в правом сыне then begin
| | поменять t с ее правым сыном; t:= правый сын
| end else begin {наибольшее число - в левом сыне}
| | поменять t с ее левым сыном; t:= левый сын
| end
end

  k := n;
  u := n;
  {все s-поддеревья с s>u регулярны }
  while u<>0 do begin
  | {u-поддерево регулярно везде, кроме разве что корня}
  | ... восстановить регулярность u-поддерева в корне;
  | u:=u-1;
  end;

Теперь запишем процедуру сортировки на паскале (предполагая, что n -- константа, x имеет тип arr = array [1..n] of integer).

  procedure sort (var x: arr);
  | var u, k: integer;
  | procedure exchange(i, j: integer);
  | | var tmp: integer;
  | | begin
  | | tmp  := x[i];
  | | x[i] := x[j];
  | | x[j] := tmp;
  | end;
  | procedure restore (s: integer);
  | | var t: integer;
  | | begin
  | | t:=s;
  | | while ((2*t+1 <= k) and (x[2*t+1] > x[t])) or
  | | |     ((2*t <= k) and (x[2*t] > x[t])) do begin
  | | | if (2*t+1 <= k) and (x[2*t+1] >= x[2*t]) then begin
  | | | | exchange (t, 2*t+1);
  | | | | t := 2*t+1;
  | | | end else begin
  | | | | exchange (t, 2*t);
  | | | | t := 2*t;
  | | | end;
  | | end;
  | end;
  begin
  | k:=n;
  | u:=n;
  | while u <> 0 do begin
  | | restore (u);
  | | u := u - 1;
  | end;
  | while k <> 1 do begin
  | | exchange (1, k);
  | | k := k - 1;
  | | restore (1);
  | end;
  end;`

Несколько замечаний

Метод, использованный при сортировке деревом, бывает полезным в других случах. (См. в главе 6 (о типах данных) об очереди с приоритетами.)

Сортировка слиянием хороша тем, что она на требует, чтобы  весь сортируемый массив помещался в оперативной памяти. Можно сначала отсортировать такие куски, которые помещаются в памяти (например, с помощью дерева), а затем сливать полученные файлы.

Еще один практически важный алгоритм сортировки (быстрая сортировка Хоара) таков:   чтобы отсортировать массив, выберем случайный его элемент b , и разобьем массив на три части: меньшие b , равные b и большие b . (Эта задача приведена в главе 1.) Теперь осталось отсортировать первую и третью части: это делается тем же способом. Время работы этого алгоритма -- случайная величина; можно доказать, что в среднем он работает не больше .На практике -- он один из самых быстрых. (Мы еще вернемся к нему, приведя его рекурсивную и нерекурсивную реализации.)

Наконец, отметим, что сортировка за время порядка может быть выполнена с помощью техники сбалансированных деревьев (см. главу 12), однако программы тут сложнее и константа C довольно велика.