Ферзи, не бьющие друг друга:
обход дерева позиций

Ферзи, не бьющие друг друга В предыдущей главе мы рассматривали несколько задач одного и того же типа: << перечислить все элементы некоторого множества A >>. Схема решения была такова: на множестве A вводился порядок и описывалась процедура перехода от произвольного элемента множества A к следующему за ним (в этом порядке). Такую схему не всегда удается реализовать непосредственно, и в этой главе мы рассмотрим другой полезный прием перечисления всех элементов некоторого множества. Его называют << поиск с возвратами>>, << метод ветвей и границ>>, << backtracking>>. На наш взгляд, наиболее точное название этого метода -- обход дерева.

$\scriptstyle{\blacktriangleright}$ 3.1.1. Перечислить все способы расстановки n ферзей на шахматной доске $n\times n$ , при которых они не бьют друг друга.

Решение. Очевидно, на каждой из n горизонталей должно стоять по ферзю. Будем называть k -позицией (для $k = 0, 1,\ldots,n$ ) произвольную расстановку k ферзей на k нижних горизонталях (ферзи могут бить друг друга). Нарисуем << дерево позиций>>: его корнем будет единственная -позиция, а из каждой k -позиции выходит n стрелок вверх в (k+1) -позиции. Эти n позиций отличаются положением ферзя на (k+1) -ой горизонтали. Будем считать, что расположение их на рисунке соответствует положению этого ферзя: левее та позиция, в которой ферзь расположен левее.

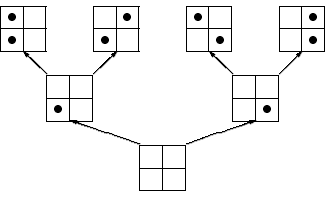$\begin{displaymath} \begin{picture} (16,9) \put(7,3){\vector(-3,1){3}} \put(9,3)... ...pbox }% \rw % \hbox{\empbox \rw \empbox }% }% }\end{picture}\end{displaymath}$ Среди позиций этого дерева нам надо отобрать те n -позиции, в которых ферзи не бьют друг друга. Программа будет << обходить дерево>> и искать их. Чтобы не делать лишней работы, заметим вот что: если в какой-то k -позиции ферзи бьют друг друга, то ставить дальнейших ферзей смысла нет. Поэтому, обнаружив это, мы будем прекращать построение дерева в этом направлении.

Точнее, назовем k -позицию допустимой, если после удаления верхнего ферзя оставшиеся не бьют друг друга. Наша программа будет рассматривать только допустимые позиции.

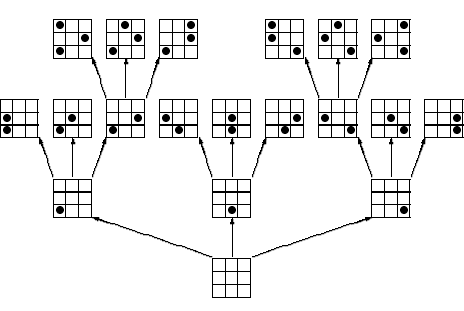
$\begin{displaymath} \begin{picture} (37,23) \put(17,4){\vector(-3,1){9}} \put(20... ... \hbox{\empbox \rw \empbox \rw \empbox }% }% }%\end{picture}\end{displaymath}$ $\begin{displaymath} {\hbox{\rm Дерево допустимых позиций для $n=3$}} \end{displaymath}$

Разобьем задачу на две части: (1) обход произвольного дерева и (2) реализацию дерева допустимых позиций.

Сформулируем задачу обхода произвольного дерева. Будем считать, что у нас имеется Робот, который в каждый момент находится в одной из вершин дерева (вершины изображены на рисунке кружочками). Он умеет выполнять команды:

вверх налево (идти по самой левой из выходящих вверх стрелок)
вправо (перейти в соседнюю справа вершину)
вниз (спуститься вниз на один уровень)

(На рисунках стрелками показано, какие перемещения соответствуют этим командам.) 0вверх налево $\begin{displaymath} \setlength {\unitlength}{12pt} \begin{picture} (8,8) \put(... ...t(5,7){\line(0,-1){2}} \put(6,7){\line(-1,-2){1}}\end{picture}\end{displaymath}$ Кроме того, в репертуар Робота входят проверки, соответствующие возможности выполнить каждую из команд:

есть_сверху;
есть_справа;
есть_снизу;

(последняя проверка истинна всюду, кроме корня). Обратите внимание, что команда вправо позволяет перейти лишь к << родному брату>>, но не к << двоюродному>>. $\begin{displaymath} \setlength {\unitlength}{1.2em} \begin{picture} (14,6) \t... ...ebox(6,1){\strut{\hbox{\rm {\bf не} действует!}}}}\end{picture}\end{displaymath}$

Будем считать, что у Робота есть команда обработать и что его задача -- обработать все листья (вершины, из которых нет стрелок вверх, то есть где условие есть_сверху ложно). Для нашей шахматной задачи команде обработать будет соответствовать проверка и печать позиции ферзей.

Доказательство правильности приводимой далее программы использует такие определения. Пусть фиксировано положение Робота в одной из вершин дерева. Тогда все листья дерева разбиваются на три категории: над Роботом, левее Робота и правее Робота. (Путь из корня в лист может проходить через вершину с Роботом, сворачивать влево, не доходя до нее и сворачивать вправо, не доходя до нее.) Через (ОЛ) обозначим условие << обработаны все листья левее Робота>>, а через (ОЛН) -- условие << обработаны все листья левее и над Роботом>>. $\begin{displaymath} \setlength {\unitlength}{1.2em} \begin{picture} (12,8) \t... ...put(8,6){\makebox(3,1){\strut{\hbox{\rm Правее}}}}\end{picture}\end{displaymath}$ Нам понадобится такая процедура:

  procedure вверх_до_упора_и_обработать
  | {дано: (ОЛ), надо: (ОЛН)}
  begin
  | {инвариант: ОЛ}
  | while есть_сверху do begin
  | | вверх_налево;
  | end
  | {ОЛ, Робот в листе}
  | обработать;
  | {ОЛН}
  end;

Основной алгоритм:

  дано: Робот в корне, листья не обработаны
  надо: Робот в корне, листья обработаны

  {ОЛ}
  вверх_до_упора_и_обработать;
  {инвариант: ОЛН}
  while есть_снизу do begin
  | if есть_справа then begin {ОЛН, есть справа}
  | | вправо;
  | | {ОЛ}
  | | вверх_до_упора_и_обработать;
  | end else begin
  | | {ОЛН, не есть_справа, есть_снизу}
  | | вниз;
  | end;
  end;
  {ОЛН, Робот в корне => все листья обработаны}

Осталось воспользоваться следующими свойствами команд Робота (в каждой строке в первой фигурной скобке записаны условия, в которых выполняется команда, во второй -- утверждения о результате ее выполнения):

(1) {ОЛ, не есть_сверху} обработать {ОЛН}

(2) {ОЛ} вверх_налево {ОЛ}

(3) {есть_справа, ОЛН} вправо {ОЛ}

(4) {не есть_справа, ОЛН} вниз {ОЛН}

$\scriptstyle{\blacktriangleright}$ 3.1.2. Доказать, что приведенная программа завершает работу (на любом конечном дереве).

Решение. Процедура вверх_налево завершает работу (высота Робота не может увеличиваться бесконечно). Если программа работает бесконечно, то, поскольку листья не обрабатываются повторно, начиная с некоторого момента ни один лист не обрабатывается. А это возможно, только если Робот все время спускается вниз. Противоречие. (Об оценке числа действий см. далее.) $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 3.1.3. Доказать правильность следующей программы обхода дерева:

 var state: (WL, WLU);
 state := WL;
 while есть_снизу or (state <> WLU) do begin
 | if (state = WL) and есть_сверху then begin
 | | вверх;
 | end else if (state = WL) and not есть_сверху then begin
 | | обработать; state := WLU;
 | end else if (state = WLU) and есть_справа then begin
 | |  вправо; state := WL;
 | end else begin {state = WLU, not есть_справа, есть_снизу}
 | |  вниз;
 | end;
 end;

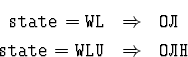
Решение. Инвариант цикла: $\begin{eqnarray*} {\hbox{\tt state}} = {\hbox{\tt WL}}&\Rightarrow& {\hbox{\tt О... ...hbox{\tt state}} = {\hbox{\tt WLU}}&\Rightarrow& {\hbox{\tt ОЛН}}\end{eqnarray*}$

Доказательство завершения работы: переход из состояния ОЛ в ОЛН возможен только при обработке вершины, поэтому если программа работает бесконечно, то с некоторого момента значение state не меняется, что невозможно. $\scriptstyle\blacktriangleleft$

$\scriptstyle{\blacktriangleright}$ 3.1.4. Решить задачу об обходе дерева, если мы хотим, чтобы обрабатывались все вершины (не только листья).

Решение. Пусть x -- некоторая вершина. Тогда любая вершина y относится к одной из четырех категорий. Рассмотрим путь из корня в y . Он может:

(а) быть частью пути из корня в x (y ниже x );

(б) свернуть налево с пути в x (y левее x );

(в) пройти через x (y над x );

(г) свернуть направо с пути в x (y правее x );

В частности, сама вершина x относится к категории (в). Условия теперь будут такими:

(ОНЛ) обработаны все вершины ниже и левее;

(ОНЛН) обработаны все вершины ниже, левее и над.

Вот как будет выглядеть программа:

  procedure вверх_до_упора_и_обработать
  | {дано: (ОНЛ), надо: (ОНЛН)}
  begin
  | {инвариант: ОНЛ}
  | while есть_сверху do begin
  | | обработать;
  | | вверх_налево;
  | end
  | {ОНЛ, Робот в листе}
  | обработать;
  | {ОНЛН}
  end;

Основной алгоритм:

  дано: Робот в корне, ничего не обработано
  надо: Робот в корне, все вершины обработаны

  {ОНЛ}
  вверх_до_упора_и_обработать;
  {инвариант: ОНЛН}
  while есть_снизу do begin
  | if есть_справа then begin {ОНЛН, есть справа}
  | | вправо;
  | | {ОНЛ}
  | | вверх_до_упора_и_обработать;
  | end else begin
  | | {ОЛН, не есть_справа, есть_снизу}
  | | вниз;
  | end;
  end;
  {ОНЛН, Робот в корне => все вершины обработаны}`

$\scriptstyle{\blacktriangleright}$ 3.1.5. Приведенная только что программа обрабатывает вершину до того, как обработан любой из ее потомков. Как изменить программу, чтобы каждая вершина, не являющаяся листом, обрабатывалась дважды: один раз до, а другой раз после всех своих потомков? (Листья по-прежнему обрабатываются по разу.)

Решение. Под << обработано ниже и левее>> будем понимать << ниже обработано по разу, слева обработано полностью (листья по разу, остальные по два)>>. Под << обработано ниже, левее и над>> будем понимать << ниже обработано по разу, левее и над -- полностью>>.

Программа будет такой:

  procedure вверх_до_упора_и_обработать
  | {дано: (ОНЛ), надо: (ОНЛН)}
  begin
  | {инвариант: ОНЛ}
  | while есть_сверху do begin
  | | обработать;
  | | вверх_налево;
  | end
  | {ОНЛ, Робот в листе}
  | обработать;
  | {ОНЛН}
  end;

Основной алгоритм:

  дано: Робот в корне, ничего не обработано
  надо: Робот в корне, все вершины обработаны

  {ОНЛ}
  вверх_до_упора_и_обработать;
  {инвариант: ОНЛН}
  while есть_снизу do begin
  | if есть_справа then begin {ОНЛН, есть справа}
  | | вправо;
  | | {ОНЛ}
  | | вверх_до_упора_и_обработать;
  | end else begin
  | | {ОЛН, не есть_справа, есть_снизу}
  | | вниз;
  | | обработать;
  | end;
  end;
  {ОНЛН, Робот в корне =>
   все вершины обработаны полностью}`

$\scriptstyle{\blacktriangleright}$ 3.1.6. Доказать, что число операций в этой программе по порядку равно числу вершин дерева. (Как и в других программах, которые отличаются от этой лишь пропуском некоторых команд обработать.)

[Указание. Примерно каждое второе действие при исполнении этой программы -- обработка вершины, а каждая вершина обрабатывается максимум дважды.] $\blacktriangleleft$

Вернемся теперь к нашей задаче о ферзях (где из всех программ обработки дерева понадобится лишь первая, самая простая). Реализуем операции с деревом позиций. Позицию будем представлять с помощью переменной k:0..n (число ферзей) и массива c: array[1..n] of 1..n (c[i] -- координаты ферзя на i-ой горизонтали; при ${\hbox{\tt i}}\gt{\hbox{\tt k}}$ значение c[i] роли не играет). Предполагается, что все позиции допустимы (если убрать верхнего ферзя, остальные не бьют друг друга).

  program queens;
  | const n = ...;
  | var
  |   k: 0..n;
  |   c: array [1..n] of 1..n;
  |
  | procedure begin_work; {начать работу}
  | begin
  | | k := 0;
  | end;
  |
  | function danger: boolean; {верхний ферзь под боем}
  | | var b: boolean; i: integer;
  | begin
  | | if k <= 1 then begin
  | | | danger := false;
  | | end else begin
  | | | b := false; i := 1;
  | | | {b <=> верхний ферзь под боем ферзей с номерами < i}
  | | | while i <> k do begin
  | | | | b := b or (c[i]=c[k]) {вертикаль}
  | | | |     or (abs(c[i]-c[k]))=abs(i-k)); {диагональ}
  | | | | i := i+1;
  | | | end;
  | | | danger := b;
  | | end;
  | end;
  |
  | function is_up: boolean {есть_сверху}
  | begin
  | | is_up := (k < n) and not danger;
  | end;
  |
  | function is_right: boolean {есть_справа}
  | begin
  | | is_right := (k > 0) and (c[k] < n);
  | end;
  | {возможна ошибка: при k=0 не определено c[k]}
  |
  | function is_down: boolean {есть_снизу}
  | begin
  | | is_down := (k > 0);
  | end;
  |
  | procedure up; {вверх_налево}
  | begin {k < n, not danger}
  | | k := k + 1;
  | | c [k] := 1;
  | end;
  |
  | procedure right; {вправо}
  | begin {k > 0,  c[k] < n}
  | | c [k] := c [k] + 1;
  | end;
  |
  | procedure down; {вниз}
  | begin {k > 0}
  | | k := k - 1;
  | end;
  |
  | procedure work; {обработать}
  | | var i: integer;
  | begin
  | | if (k = n) and not danger then begin
  | | | for i := 1 to n do begin
  | | | | write ('<', i, ',' , c[i], '> ');
  | | | end;
  | | | writeln;
  | | end;
  | end;
  |
  | procedure UW; {вверх_до_упора_и_обработать}
  | begin
  | | while is_up do begin
  | | | up;
  | | end
  | | work;
  | end;
  |
  begin
  | begin_work;
  | UW;
  | while is_down do begin
  | | if is_right then begin
  | | | right;
  | | | UW;
  | | end else begin
  | | | down;
  | | end;
  | end;
  end;`

0есть_сверху 1есть_сверху

$\scriptstyle{\blacktriangleright}$ 3.1.7. Приведенная программа тратит довольно много времени на выполнение проверки 0 (проверка, находится ли верхний ферзь под боем, требует числа действий порядка n). Изменить реализацию операций с деревом позиций так, чтобы все три проверки 1/справа/снизу и соответствующие команды требовали бы количества действий, ограниченного не зависящей от n константой.

Решение. Для каждой вертикали, каждой восходящей и каждой нисходящей диагонали будем хранить булевское значение -- сведения о том, находится ли на этой линии ферзь (верхний ферзь не учитывается). (Заметим, что в силу допустимости позиции на каждой из линий может быть не более одного ферзя.). $\scriptstyle\blacktriangleleft$

pvv
1/8/1999

Ферзи, не бьющие друг друга: обход дерева позиций

Ферзи, не бьющие друг друга:
обход дерева позиций