3.1. Хеширование данныхДля ускорения доступа к данным в таблицах можно использовать предварительное упорядочивание таблицы в соответствии со значениями ключей.
При этом могут быть использованы методы поиска в упорядоченных структурах данных, например, метод половинного деления, что существенно сокращает время поиска данных по значению ключа. Однако при добавлении новой записи требуется переупорядочить таблицу. Потери времени на повторное упорядочивание таблицы могут значительно превышать выигрыш от сокращения времени поиска. Поэтому для сокращения времени доступа к данным в таблицах используется так называемое случайное упорядочивание или хеширование. При этом данные организуются в виде таблицы при помощи хеш-функции h, используемой для ⌠вычисления■ адреса по значению ключа.
Рис.3.1. Хеш-таблица
Идеальной хеш-функцией является такая hash-функция, которая для любых двух неодинаковых ключей дает неодинаковые адреса.
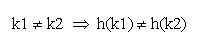
Подобрать такую функцию можно в случае, если все возможные значения ключей заранее известны. Такая организация данных носит название ⌠совершенное хеширование⌠. В случае заранее неопределенного множества значений ключей и ограниченной длины таблицы подбор совершенной функции затруднителен. Поэтому часто используют хеш-функции, которые не гарантируют выполнение условия.
Рассмотрим пример реализации несовершенной хеш-функции на языке TurboPascal. Предположим, что ключ состоит из четырех символов. При этом таблица имеет диапазон адресов от 0 до 10000.
function hash (key : string[4]): integer;
var
f: longint;
begin
f:=ord (key[1]) - ord (key[2]) + ord (key[3]) -ord (key[4]);
{вычисление функции по значению ключа}
f:=f+255*2;
{совмещение начала области значений функции с начальным
адресом хеш-таблицы (a=1)}
f:=(f*10000) div (255*4);
{совмещение конца области значений функции с конечным адресом
хеш-таблицы (a=10 000)}
hash:=f
end;
При заполнении таблицы возникают ситуации, когда для двух неодинаковых ключей функция вычисляет один и тот же адрес. Данный случай носит название ⌠коллизия■, а такие ключи называются ⌠ключи-синонимы■.
3.1.1. Методы разрешения коллизийДля разрешения коллизий используются различные методы, которые в основном сводятся к методам ⌠цепочек⌠ и ⌠открытой адресации⌠.
Методом цепочек называется метод, в котором для разрешения коллизий во все записи вводятся указатели, используемые для организации списков √ ⌠цепочек переполнения■. В случае возникновения коллизии при заполнении таблицы в список для требуемого адреса хеш-таблицы добавляется еще один элемент.
Поиск в хеш-таблице с цепочками переполнения осуществляется следующим образом. Сначала вычисляется адрес по значению ключа. Затем осуществляется последовательный поиск в списке, связанном с вычисленным адресом.
Процедура удаления из таблицы сводится к поиску элемента и его удалению из цепочки переполнения.
Рис.3.2. Разновидности методов разрешение коллизий
Рис.3.3. Разрешение коллизий при добавлении элементов методом цепочек
Метод открытой адресации состоит в том, чтобы, пользуясь каким-либо алгоритмом, обеспечивающим перебор элементов таблицы, просматривать их в поисках свободного места для новой записи.
Рис.3.4. Разрешение коллизий при добавлении элементов методами открытой адресации.
Линейное опробование сводится к последовательному перебору элементов таблицы с некоторым фиксированным шагом
a=h(key) + c*i ,
где i √ номер попытки разрешить коллизию. При шаге равном единице происходит последовательный перебор всех элементов после текущего.
Квадратичное опробование отличается от линейного тем, что шаг перебора элементов не линейно зависит от номера попытки найти свободный элемент
a = h(key2) + c*i + d*i 2
Благодаря нелинейности такой адресации уменьшается число проб при большом числе ключей-синонимов.
Однако даже относительно небольшое число проб может быстро привести к выходу за адресное пространство небольшой таблицы вследствие квадратичной зависимости адреса от номера попытки.
Еще одна разновидность метода открытой адресации, которая называется двойным хешированием, основана на нелинейной адресации, достигаемой за счет суммирования значений основной и дополнительной хеш-функций
a=h1(key) + i*h2(key).
Опишем алгоритмы вставки и поиска для метода линейное опробование.
Вставка
- i = 0
- a = h(key) + i*c
- Если t(a) = свободно, то t(a) = key, записать элемент, стоп элемент добавлен
- i = i + 1, перейти к шагу 2
Поиск
- i = 0
- a = h(key) + i*c
- Если t(a) = key, то стоп элемент найден
- Если t(a) = свободно, то стоп элемент не найден
- i = i + 1, перейти к шагу 2
Аналогичным образом можно было бы сформулировать алгоритмы добавления и поиска элементов для любой схемы открытой адресации. Отличия будут только в выражении, используемом для вычисления адреса
(шаг 2). С процедурой удаления дело обстоит не так просто, так как она в данном случае не будет являться обратной процедуре вставки.
Дело в том, что элементы таблицы находятся в двух состояниях: свободно и занято. Если удалить элемент, переведя его в состояние свободно, то после такого удаления алгоритм поиска будет работать некорректно. Предположим, что ключ удаляемого элемента имеет в таблице ключи синонимы. В том случае, если за удаляемым элементом в результате разрешения коллизий были размещены элементы с другими ключами, то поиск этих элементов после удаления всегда будет давать отрицательный результат, так как алгоритм поиска останавливается на первом элементе, находящемся в состоянии свободно.
Скорректировать эту ситуацию можно различными способами. Самый простой из них заключается в том, чтобы производить поиск элемента не до первого свободного места, а до конца таблицы. Однако такая модификация алгоритма сведет на нет весь выигрыш в ускорении доступа к данным, который достигается в результате хеширования.
Другой способ сводится к тому, чтобы проследить адреса всех ключей-синонимов для ключа удаляемого элемента и при необходимости пере разместить соответствующие записи в таблице. Скорость поиска после такой операции не уменьшится, но затраты времени на само пере размещение элементов могут оказаться очень значительными.
Существует подход, который свободен от перечисленных недостатков. Его суть состоит в том, что для элементов хеш-таблицы добавляется состояние ⌠удалено■. Данное состояние в процессе поиска интерпретируется, как занято, а в процессе записи как свободно.
Сформулируем алгоритмы вставки поиска и удаления для хеш-таблицы, имеющей три состояния элементов.
Вставка
- i = 0
- a = h(key) + i*c
- Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
- i = i + 1, перейти к шагу 2
Удаление
- i = 0
- a = h(key) + i*c
- Если t(a) = key, то t(a) =удалено, стоп элемент удален
- Если t(a) = свободно, то стоп элемент не найден
- i = i + 1, перейти к шагу 2
Поиск
- i = 0
- a = h(key) + i*c
- Если t(a) = key, то стоп элемент найден
- Если t(a) = свободно, то стоп элемент не найден
- i = i + 1, перейти к шагу 2
Алгоритм поиска для хеш-таблицы, имеющей три состояния, практически не отличается от алгоритма поиска без учета удалений. Разница заключается в том, что при организации самой таблицы необходимо отмечать свободные и удаленные элементы. Это можно сделать, зарезервировав два значения ключевого поля. Другой вариант реализации может предусматривать введение дополнительного поля, в котором фиксируется состояние элемента. Длина такого поля может составлять всего два бита, что вполне достаточно для фиксации одного из трех состояний. На языке TurboPascal данное поле удобно описать типом Byte или Char.
3.1.2. Переполнение таблицы и рехеширование
Очевидно, что по мере заполнения хеш-таблицы будут происходить коллизии и в результате их разрешения методами открытой адресации очередной адрес может выйти за пределы адресного пространства таблицы. Что бы это явление происходило реже, можно пойти на увеличение длины таблицы по сравнению с диапазоном адресов, выдаваемым хеш-функцией.
Рис.3.5. Циклический переход к началу таблицы.
С одной стороны это приведет к сокращению числа коллизий и ускорению работы с хеш-таблицей, а с другой √ к нерациональному расходованию адресного пространства. Даже при увеличении длины таблицы в два раза по сравнению с областью значений хеш-функции нет гарантии того, что в результате коллизий адрес не превысит длину таблицы. При этом в начальной части таблицы может оставаться достаточно свободных элементов. Поэтому на практике используют циклический переход к началу таблицы.
Рассмотрим данный способ на примере метода линейного опробования. При вычислении адреса очередного элемента можно ограничить адрес, взяв в качестве такового остаток от целочисленного деления адреса на длину таблицы n.
Вставка
- i = 0
- a = (h(key) + c*i) mod n
- Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
- i = i + 1, перейти к шагу 2
В данном алгоритме мы не учитываем возможность многократного превышения адресного пространства. Более корректным будет алгоритм, использующий сдвиг адреса на 1 элемент в случае каждого повторного превышения адресного пространства. Это повышает вероятность найти свободные элементы в случае повторных циклических переходов к началу таблицы.
Вставка
- i = 0
- a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
- Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
- i = i + 1, перейти к шагу 2
- a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
Рассматривая возможность выхода за пределы адресного пространства таблицы, мы не учитывали факторы заполненности таблицы и удачного выбора хеш-функции. При большой заполненности таблицы возникают частые коллизии и циклические переходы в начало таблицы. При неудачном выборе хеш-функции происходят аналогичные явления. В наихудшем варианте при полном заполнении таблицы алгоритмы циклического поиска свободного места приведут к зацикливанию. Поэтому при использовании хеш-таблиц необходимо стараться избегать очень плотного заполнения таблиц. Обычно длину таблицы выбирают из расчета двукратного превышения предполагаемого максимального числа записей. Не всегда при организации хеширования можно правильно оценить требуемую длину таблицы, поэтому в случае большой заполненности таблицы может понадобиться рехеширование. В этом случае увеличивают длину таблицы, изменяют хеш-функцию и переупорядочивают данные.
Производить отдельную оценку плотности заполнения таблицы после каждой операции вставки нецелесообразно, поэтому можно производить такую оценку косвенным образом √ по числу коллизий во время одной вставки. Достаточно определить некоторый порог числа коллизий, при превышении которого следует произвести рехеширование. Кроме того, такая проверка гарантирует невозможность зацикливания алгоритма в случае повторного просмотра элементов таблицы.
Рассмотрим алгоритм вставки, реализующий предлагаемый подход.
Вставка
- i = 0
- a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
- Если t(a) = свободно или t(a) = удалено, то t(a) = key, записать элемент, стоп элемент добавлен
- Если i > m , то стоп требуется рехеширование
- i = i + 1, перейти к шагу 2
В данном алгоритме номер итерации сравнивается с пороговым числом m. Следует заметить, что алгоритмы вставки, поиска и удаления должны использовать идентичное образование адреса очередной записи.
Удаление
- i = 0
- a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
- Если t(a) = key, то t(a) =удалено, стоп элемент удален
- Если t(a) = свободно или i>m, то стоп элемент не найден
- i = i + 1, перейти к шагу 2
Поиск
3.1.3. Оценка качества хеш-функции
- i = 0
- a = ((h(key) + c*i) div n + (h(key) + c*i) mod n) mod n
- Если t(a) = key, то стоп элемент найден
- Если t(a) = свободно или i>m, то стоп элемент не найден
- i = i + 1, перейти к шагу 2
Как уже было отмечено, очень важен правильный выбор хеш-функции. При удачном построении хеш-функции таблица заполняется более равномерно, уменьшается число коллизий и уменьшается время выполнения операций поиска, вставки и удаления. Для того чтобы предварительно оценить качество хеш-функции можно провести имитационное моделирование. Моделирование проводится следующим образом. Формируется целочисленный массив, длина которого совпадает с длиной хеш-таблицы. Случайно генерируется достаточно большое число ключей, для каждого ключа вычисляется хеш-функция. В элементах массива просчитывается число генераций данного адреса. По результатам такого моделирования можно построить график распределения значений хеш-функции. Для получения корректных оценок число генерируемых ключей должно в несколько раз превышать длину таблицы.
Рис. 3.6. Распределение коллизий в адресном пространстве таблицы
Если число элементов таблицы достаточно велико, то график строится не для отдельных адресов, а для групп адресов. Например, все адресное пространство разбивается на 100 фрагментов и подсчитывается число попаданий адреса для каждого фрагмента. Большие неравномерности свидетельствуют о высокой вероятности коллизий в отдельных местах таблицы. Разумеется, такая оценка является приближенной, но она позволяет предварительно оценить качество хеш-функции и избежать грубых ошибок при ее построении.
Оценка будет более точной, если генерируемые ключи будут более близки к реальным ключам, используемым при заполнении хеш-таблицы. Для символьных ключей очень важно добиться соответствия генерируемых кодов символов тем кодам символов, которые имеются в реальном ключе. Для этого стоит проанализировать, какие символы могут быть использованы в ключе.
Например, если ключ представляет собой фамилию на русском языке, то будут использованы русские буквы. Причем первый символ может быть большой буквой, а остальные √ малыми. Если ключ представляет собой номерной знак автомобиля, то также несложно определить допустимые коды символов в определенных позициях ключа.
Рассмотрим пример генерации ключа из десяти латинских букв, первая из которых является большой, а остальные √малыми.
Пример
: ключ √ 10 символов, 1-й большая латинская буква2-10 малые латинские буквы
var i:integer; s:string[10];
begin
s[1]:=chr(random(90-65)+65);
for i:=2 to 10 do s[i]:=chr(random(122-97)+97);
end
В данном фрагменте используется тот факт, что допустимые коды символов располагаются последовательными непрерывными участками в кодовой таблице. Рассмотрим более общий случай. Допустим, необходимо сгенерировать ключ из m символов с кодами в диапазоне от n1 до n2.
Генерация ключа из m символов c кодами в диапазоне от n1 до n2
(диапазон непрерывный)
for i:=1 to m do str[i]:=chr(random(n2-n1)+n1);
На практике возможны варианты, когда символы в одних позициях ключа могут принадлежать к разным диапазонам кодов, причем между этими диапазонами может существовать разрыв.
Генерация ключа из m символов c кодами
в диапазоне от n1 до n4 (диапазон имеет разрыв от n2 до n3)
for i:=1 to m do
begin
x:=random((n4 - n3) + (n2 √ n1));
if x<=(n2 - n1) then str[i]:=chr(x + n1)
else str[i]:=chr(x + n1 + n3 √ n2)
end;
Рассмотрим еще один конкретный пример. Допустим известно, что ключ состоит из 7 символов. Из них три первые символа √ большие латинские буквы, далее идут две цифры, остальные √ малые латинские.
Пример: длина ключа 7 символов
- 3 большие латинские (коды 65-90)
- 2 цифры (коды 48-57)
- 2 малые латинские (коды 97-122)
var
key: string[7];
begin
for i:=1 to 3 do key[i]:=chr(random(90-65)+65);
for i:=4 to 5 do key[i]:=chr(random(57-48)+57);
for i:=6 to 7 do key[i]:=chr(random(122-97)+97);
end;
В рассматриваемых примерах мы исходили из предположения, что хеширование будет реализовано на языке Turbo Pascal, а коды символов соответствуют альтернативной кодировке.
3.2. Организация данных для ускорения поиска по вторичным ключам
До сих пор рассматривались способы поиска в таблице по ключам, позволяющим однозначно идентифицировать запись. Мы будем называть такие ключи первичными ключами. Возможен вариант организации таблицы, при котором отдельный ключ не позволяет однозначно идентифицировать запись. Такая ситуация часто встречается в базах данных. Идентификация записи осуществляется по некоторой совокупности ключей. Ключи, не позволяющие однозначно идентифицировать запись в таблице, называются вторичными ключами.
Даже при наличии первичного ключа, для поиска записи могут быть использованы вторичные. Например, поисковые системы internet часто организованы как наборы записей, соответствующих Web-страницам. В качестве вторичных ключей для поиска выступают ключевые слова, а сама задача поиска сводится к выборке из таблицы некоторого множества записей, содержащих требуемые вторичные ключи.
3.2.1. Инвертированные индексыРассмотрим метод организации таблицы с инвертированными индексами. Для таблицы строится отдельный набор данных, содержащий так называемые инвертированные индексы. Вспомогательный набор содержит для каждого значения вторичного ключа отсортированный список адресов записей таблицы, которые содержат данный ключ.
Поиск осуществляется по вспомогательной структуре достаточно быстро, так как фактически отсутствует необходимость обращения к основной структуре данных. Область памяти, используемая для индексов,
является относительно небольшой по сравнению с другими методами организации таблиц.
Рис.3.7. Метод организации таблицы с инвертированными индексами
Недостатками данной системы являются большие затраты времени на составление вспомогательной структуры данных и ее обновление. Причем эти затраты возрастают с увеличение объема базы данных.
Система инвертированных индексов является чрезвычайно удобной и эффективной при организации поиска в больших таблицах.
3.2.2. Битовые картыДля таблиц небольшого объема используют организацию вспомогательной структуры данных в виде битовых карт. Для каждого значения вторичного ключа записей основного набора данных записывается последовательность битов. Длина последовательности битов равна числу записей. Каждый бит в битовой карте соответствует одному значению вторичного ключа и одной записи. Единица означает наличие ключа в записи, а ноль √отсутствие.
Рис.3.8. Организация вспомогательной структуры данных в виде битовых карт
Основным преимуществом такой организации является очень простая и эффективная организация обработки сложных запросов, которые могут объединять значения ключей различными логическими предикатами. В этом случае поиск сводится к выполнению логических операций запроса непосредственно над битовыми строками и интерпретации результирующей битовой строки. Другим преимуществом является простота обновления карты при добавлении записей.
К недостаткам битовых карт следует отнести увеличение длины строки пропорционально длине файла. При этом заполненность карты единицами уменьшается с увеличением длины файла. Для большой длине таблицы и редко встречающихся ключах битовая карта превращается в большую разреженную матрицу, состоящую в основном из одних нулей.