 |
|
Математика : Графы.
Минимальное остовное дерево.
перевод Кантор И.
автор неизвестен
Примем без доказательства следующее свойство MST ( minimal spanning tree - минимальное остовное дерево на англ.).
В графе G=(V, E) рассмотрим U - некоторое подмножество V, такое что U и V-U не пусты. Пусть (u, v) - ребро наименьшей стоимости, одна вершина которого - u принадлежит U, а другая - v принадлежит V-U. Тогда существует некоторое MST, содержащее ребро (u, v).
Пусть в примере ниже U = B, C. Тогда существует MST, содержащее ребро (C, E).
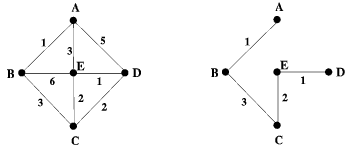
На этом свойстве основаны два известных алгоритма.
Алгоритм Прима.
Начинаем с пустого U=0. Добавляем к U вершины, каждый раз находя ребро наименьшей стоимости между U и V-U.
Положить в U любую вершину; // изначально U - пусто.
while ( V-U не пусто )
{
Выбрать ребро (u, v) наименьшей стоимости,
u из U, v из V-U;
Добавить v к U (и убрать из V-U);
}
Очевидно, данный алгоритм имеет сложность O(V2)
Алгоритм Краскала.
В отличие от алгоритма Прима, этот алгоритм не требует прохода по всем вершинам для нахождения ребра с минимальным весом. Вместо этого он использует 'жадный' подход.
Работаем с вершинами, а не с ребрами G. Это дает нам V связных компонент. Будем увеличивать их размер по ребру за раз. Число ребер, необходимое для остовного дерева: V-1. Граф связен, а значит E содержит как минимум такое их количество.
Создаем список вершин L, в неубывающем по весу порядке
while ( число отмеченных вершин < V-1 )
{
w = L.Remove(); // удалить из головы списка
if ( w соединяет две несвязных компоненты )
отметить w и добавить к MST
else // w - внутри компоненты
не отмечать w // это приведет к циклу в MST
}
Сложность алгоритма составляет O(E*lg E).
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.