 |
|
Математика : Графы.
Hахождение кpатчайших пyтей в гpафе. Волновой алгоритм.
Дано: непyстой гpаф G=(V,E). Требуется найти путь между вершинами s и t графа (s не совпадает с t), содержащий минимальное количество промежуточных вершин (ребер).
I.
- каждой вершине vi приписывается целое число T(vi) - волновая метка (начальное значение T(vi)=-1);
- заводятся два списка OldFront и NewFront (старый и новый "фpонт волны"), а также пеpеменная T (текyщее вpемя);
- OldFront:={s}; NewFront:={}; T(s):=0; T:=0;
- для каждой из веpшин, входящих в OldFront, пpосматpиваются инцидентные (смежные) ей веpшины uj, и если T(uj) = -1, то T(uj):=T+1, NewFront:=NewFront + {uj};
- если NewFront = {}, то ВЫХОД("нет решения");
- если t О NewFront (т.е. одна из веpшин uj совпадает t), то найден кpатчайший пyть между s и t с T(t)=T+1 промежуточными ребрами; ВЫХОД("решение найдено");
- OldFront:=NewFront; NewFront:={}; T:=T+1; goto (4).
II.
Если на шаге (6) была достигнyта веpшина t, то восстановить кpатчайший пyть можно следyющим обpазом: сpеди соседей веpшины t найдем любую веpшину с волновой меткой T(t)-1, сpеди соседей последней - веpшину с меткой T(t)-2, и т.д., пока не достигнем s. Найденная последовательность вершин определяет один из кpатчайших пyтей из s в t. Hа пpактике выгодно сохpанять на шаге (4) инфоpмацию о том, из какой веpшины "волна" пpишла в веpшинy uj - тогда восстановление пyти осyществляется быстpее.
Под корректностью алгоритма здесь понимается, что:
A.
Волновой алгоритм завершает работу за конечное число итераций - это следует из конечности графа, а также из того, что на каждой итерации либо происходит уменьшение количества вершин графа, волновая метка которых равна "-1" (на шаге 4), либо завершение работы алгоритма (на шаге 5).
B.
1. Докажем по индукции, что (*) к началу выполнения шага (4) алгоритма при заданном значении T волновые метки всех вершин vi, таких, что расстояние (т.е. количество ребер в кратчайшем пути) между s и vi равно T, также равны T ((d(s,vi)=T) => (T(vi)=T)), и, кроме того, все эти вершины находятся в списке OldFront. Базис индукции: при T=0 утверждение (*) выполняется (единственной вершиной, находящейся на расстоянии 0 от s, является сама вершина s; на шаге (3) она получит волновую метку 0 и будет занесена в OldFront); при T=1 утверждение (*) также выполняется (т.к. при T=0 все вершины, инцидентные s, получат волновую метку 1 и попадут сначала в NewFront, а затем, на шаге (7) алгоритма, в OldFront). Допустим, что (**) утверждение (*) выполняется для всех T<T0 (T0>1). Рассмотрим все вершины uj, находящиеся на расстоянии T0 от s: d(s,uj)=T0. Запишем кратчайший путь из s в uj в виде L=(s(s,w1)w1...(wk,uj)uj), где k=T0-1. Путь L'=(s(s,w1)w1...(wk-1,wk)wk) является кратчайшим путем из s в wk (в противном случае L не являлся бы кратчайшим путем из s в uj), его длина T'=T0-1<T0, поэтому в силу (**) к началу выполнения шага (4) алгоритма при T=T', во-первых, T(wk)=T', и, во-вторых, wk находится в OldFront. Вершины wk и uj являются смежными, поэтому на шаге (4) вершина uj получит волновую метку T'+1=T0 и попадет в NewFront. На шаге (7) значение T будет увеличено на единицу, а NewFront скопирован в OldFront, следовательно, утверждение (*) будет выполняться при T=T0.
2. Поскольку при работе алгоритма T "пробегает" все целые значения, начиная с 0 и кончая некоторым целым числом, большим либо равным 0, из 1 следует, что если волновая метка вершины не равна -1, то она равна расстоянию между s и этой вершиной ((T(vi)=a, a =/= -1) => (d(s,vi)=a)).
3. Докажем, что (*) если решение существует, т.е. существует кратчайший путь из s в t длины d(s,t), то выполнение шага (4) при T'=d(s,t)-1 будет иметь место. Единственной возможностью для завершения работы алгоритма при некотором T''<T' является выход на шаге (5), но такой выход возможен тогда и только тогда, когда (**) ни одна из вершин, находящихся на расстоянии T'' от s, не имеет инцидентных вершин, находящихся на расстоянии, большем T'', от s. Действительно, выход на шаге (5) происходит, если и только если список NewFront пуст, а это возможно, если и только если на данной итерации все вершины, инцидентные вершинам из OldFront, имеют волновые метки, не равные -1. Волновые метки этих вершин не могут быть больше T'' (т.к. отличные от -1 значения были присвоены им на итерациях алгоритма при T<T''), следовательно, волновые метки находятся в диапазоне [0..T'']. В силу 2 волновые метки вершин, не равные -1, равны расстояниям между s и этими вершинами, что и доказывает (**). Из (**) cледует, что путей между s и вершинами, находящимися на расстоянии T>T'', в том числе между s и t, не существует. Значит, выход на шаге (5) при T''<T' не может произойти и утверждение (*) верно.
4. Из 1-3 следует: (*) волновые метки вершин vi, находящихся на расстоянии, меньшем d(s,t), от s, равны этому расстоянию ((d(vi,s)<d(s,t)) => (T(vi)=d(vi,s))); (**) на некоторой итерации вершина t получит волновую метку d(s,t) и попадет в NewFront, следовательно, алгоритм завершится на шаге (6) той же итерации. Корректность используемого способа восстановления кратчайшего пути по волновым меткам вершин следует из (*).
Существуют модификации приведенного здесь алгоритма, позволяющие находить:
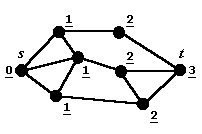
Разметка графа после выполнения волнового алгоритма.
Доказательство корректности волнового алгоритма
А. алгоритм завершает работу за конечное время;
Будем называть итерацией волнового алгоритма очередное выполнение шагов (4)-(7) алгоритма.
B. если решение существует, то алгоритм находит правильное решение.
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.
