Поиск по сайту.

Игры, и все с ними связанное.

Smart Moves: Intelligent Pathfinding.

'Алгоритмы поиска пути'

Original article © Brian Stout, 1997
Translation into Russian © Maxim Kamensky, 2000
Оригинал перевода и возможные дополнения на skael.nm.ru

Обход препятствий
Поиск пути на графе
Алгоритм А*
Непрерывное игровое пространство

Хотя поиск пути не тривиальная задача, существует несколько хороших, надежных алгоритмов, которые заслуживают большей известности в сообществе разработчиков.

Некоторые алгоритмы поиска пути не очень эффективны, но их изучение позволяет постепенно вводить концепции. Так можно понять, как решаются различные проблемы.

Типичной проблемой в поиске пути является обход препятствий. Наипростейшим подходом к проблеме является игнорирование препятствий до столкновения с ними. Такой алгоритм будет выглядеть примерно так:


Пока не цель не достигнута
	Выбрать направление для движения к цели
	Если это направление свободно для движения
		Двигаться туда
	Иначе
		Выбрать другое направление в
		соответсвии со стратегией обхода

Этот подход прост, так как он предъявляет совсем немного требований: все, что необходимо знать - это относительные положения объекта и его цели, и признак блокирования препятствием. Для многих игровых ситуаций этого достаточно.

Различные стратегии обхода препятсвий включают в себя:

Перемещение в случайном направлении. Если препятствия маленькие и выпуклые, объект (показан зеленой точкой) может, вероятно, обойти их путем небольшого смещения в сторону до тех пор, пока не достигнет цели (показана красной точкой). Рисунок 1А показывает, как работает такая стратегия. Проблемы у этого метода возникают, если препятствия большие или вогнутые, как показано на рисунке 1Б - объект может полностью застрять или как минимум потерять много времени, пока не будет найден обходной путь. Существует только один способ избежать этого: если проблему очень трудно преодолеть, то измените игру так, чтобы эта проблема никогда не возникала. То есть, убедитесь, что в игре никогда не будет вогнутых объектов.

Рис. 1А

Рис. 1Б.

Трассировка вокруг препятствия. К счастью, существуют другие методы обхода. Если препятствие большое, можно коснуться рукой препятствия и следовать контуру препятствия, пока она не обойдено. Рисунок 2А показывает, как хорошо этот метод работает с большими препятствиями. Проблема с этим методом состоит в принятии решения - когда же прекратить трассировку. Типичной эвристикой может быть: "Остановить трассировку при передвижении в направлении, которое было желаемым в начале трассировки". Это будет работать во многих случаях, однако рисунок 2Б показывает, как можно постоянно кружить внутри препятствия не находя пути наружу.

Рис. 2А.

Рис. 2Б.

Надежная трассировка. Более надежная эвристика пришла из работ над мобильными роботами: "При блокировании, вычислить уравнение линии из текущей позиции к цели. Трассировать до тех пор, пока эта линия не пересечена снова. Прервать работу, если вы опять попали в начальную позицию". Этот метод гарантирует нахождение пути вокруг препятствия, если он есть, что показано на рисунке 3А. (Если изначальная точка блокирования между вами и целью при пересечении линии, ни в коем случае не останавливайте трассировку, чтобы избежать дальнейшего зацикливания) Рисунок 3Б показывает обратную сторону этого подхода: зачастую требуется гораздо больше времени на трассировку чем необходимо. Компромисс состоит в комбинации обоих подходов: всегда использовать эвристику попроще для остановки трассирования, но если зафиксировано зацикливание, переключаться на надежную эвристику.

Рис. 3А.

Рис. 3Б.

Хотя техники обхода препятствий рассмотренные выше часто могут проделать допустимую или даже адекватную работу, существуют ситуации, в которых единственно разумный подход это планирование всего пути перед началом перемещений. В дополнение, эти методы не могут решить проблему взвешенных областей, которая состоит не столько в обходе препятствий, сколько в поиске пути с наименьшей стоимостью среди других вариантов, где стоимость местности может изменяться.

К счастью, в областях теории графов и обычного ИИ имеется несколько алгоритмов, которые могут решить проблему и сложных препятствий и взвешенных областей. В литературе, многие из этих алгоритмов представлены в терминах изменения состояний или прохода по узлам графа. Это зачастую используется для решения множества проблем, включая "пятнашки" и кубик Рубика, где состоянием является сочетание цифр или кубиков, и соседние состояния (или смежные узлы) посещаются путем перемещения цифр или поворота граней кубика. Применение этих алгоритмов к поиску пути в геометрическом пространстве требует простой адаптации: состояние или узел графа представляют объект, находящийся в определенной клетке, и передвижение в соседние клетки соответствует перемещению в соседние состояния или смежные узлы.

Рассматривая алгоритмы от простейших к более надежным, имеем:

Поиск в ширину. Начиная со стартового узла, этот алгоритм сначала определяет все непосредственно соседние узлы, затем все узлы в двух шагах, затем в трех, и так далее, пока цель не достигнута. Типичным является то, что для каждого узла его непроверенные соседи помещаются в список Open, который обычно является FIFO очередью. Алгоритм может работать так, как показано в Листинге 1. Рисунок 4 демонстрирует процесс поиска. Можно заметить, что он находит путь вокруг препятствий, и этот путь является кратчайшим, то есть одним из нескольких кратчайших в длину путей, если все шаги имеют одинаковую стоимость. Тут имеется множество простых проблем. Одна заключается в том, что поиск идет равномерно во всех направлениях, вместо того, чтобы быть направленным в сторону цели. Другая проблема в том, что не все шаги равны, по крайней мере, шаги по диагонали должны быть длиннее ортогональных.

Рис. 4.

Двунаправленный поиск в ширину. Это улучшает простой поиск в ширину тем, что запускаются два одновременных поиска в ширину из стартового и конечного узлов и останавливается, когда узел из одного фронта поиска находит соседний узел из другого фронта. Как показано на рисунке 5, это может улучшить простой поиск в ширину (обычно в 2 раза), но все еще является очень неэффективным. Хитрости, наподобие этой, хорошо запомнить, так как они могут пригодиться в дальнейшем.

Рис. 5.

Алгоритм Дийкстры. Е. Дийкстра разработал классический алгоритм для прохода по графам, грани которых имеют различный вес. На каждом шаге, он ищет необработанные узлы близкие к стартовому, затем просматривает соседей найденного узла, и устанавливает или обновляет их соответствующие расстояния от старта. Этот алгоритм имеет два преимущества по сравнению с поиском в ширину: он принимает во внимание стоимость или длину пути и обновляет узлы, если к ним найден лучший путь. Для реализации, список Open с очередью FIFO заменяется приоритетной очередью, где извлеченный узел имеет лучшее значение - здесь, это наименьшая стоимость пути от старта. (См. листинг 2.) На рисунке 6 показана хорошая адаптация алгоритма к стоимости местности. Однако, он имеет слабость поиска в ширину, игнорируя направление к цели.

Рис. 6.

Поиск в глубину. Этот поиск противоположен поиску в ширину. Вместо посещения вначале всех соседей, а потом их наследников, он сначала посещает всех наследников, а только затем переключается на соседей. Для уверенности в том, что поиск закончится, необходимо предусмотреть остановку на определенной глубине. Можно использовать тот же самый код, что и в поиске в ширину, если добавить параметр для отслеживания глубины каждого узла и заменить Open с очереди FIFO на стек LIFO (last-in-first-out). На самом деле можно полностью избавиться от списка Open и вместо этого сделать поиск рекурсивной подпрограммой, что уменьшит расход памяти использованной под Open. Необходимо, чтобы каждая ячейка маркировалась как "посещенная" при продвижении в глубь и эта пометка снималась на обратном ходу, чтобы избежать генерации путей, которые посещают дважды одну и ту же ячейку. На рисунке 7 можно заметить, что этого недостаточно, алгоритм все равно может путаться вокруг себя и тратить время на бессмысленные пути. Для геометрического поиска пути можно сделать два дополнения. Первое будет заключаться в добавлении метки на каждую ячейку с длиной найденного к ней кратчайшего пути; алгоритм больше не посетит эту ячейку пока не будет иметь к ней путь с меньшей стоимостью. Другое заключается в выборе вначале соседей, которые ближе к цели. С этими двумя дополнениями, можно заметить, что поиск в глубину быстро найдет путь. Могут обрабатываться даже взвешенные пути, если сделать остановку по общей накопленной стоимости вместо общего расстояния.

Рис. 7.

Алгоритм последовательных приближений при поиске в глубину (IDDFS). В действительности в алгоритме поиска в глубину существует еще одна проблема - выбор правильной глубины остановки. Если она будет слишком маленькой, то путь не будет найден; если слишком большой, то потенциально можно потратить много времени впустую, исследуя слишком глубоко, или найти путь с очень высокой стоимостью. Эти проблемы решаются итеративным углублением - техника, при которой выполняется поиск в глубину с увеличивающейся глубиной до тех пор, пока путь не будет найден. При поиске пути мы можем не начинать с глубины равной единице, а сразу начать с глубины равной расстоянию по прямой от старта к цели. Этот поиск является асимптотически оптимальным среди всех переборных алгоритмов по времени и памяти.

Алгоритм “лучший-первый”. Это первый рассматриваемый эвристический поиск, который принимает во внимание знания о пространстве поиска для направления своих усилий. Он похож на алгоритм Дийкстры, за исключением того, что узлы в списке Open оцениваются по приблизительному оставшемуся расстоянию до цели. Эта оценка так же не требует наличия обновлений, в отличие от алгоритма Дийкстры. Рисунок 8 показывает работу алгоритма. Это самый быстрый из всех планирующих алгоритмов рассмотренных ранее, который направляется по прямой к цели. Он так же имеет и свои слабости. На рисунке 8А, показано, что он не принимает во внимание накопленную стоимость пути, направляясь по прямой через зону с высокой стоимостью, а не обходя ее. И на рисунке 8Б можно увидеть, что найденный путь вокруг препятствия не прямой, а изгибается вокруг препятствия на манер алгоритма трассировки, рассмотренного ранее.

Рис. 8А.

Рис. 8Б.

Алгоритм А*

Наилучшим алгоритмом для поиска оптимальных путей в различных пространствах является A* (читается как "А-звездочка"). Этот эвристический поиск сортирует все узлы по приближению наилучшего маршрута, идущего через этот узел. Типичная формула эвристики выражается в виде:

f(n) = g(n) + h(n)

где:

f(n) значение оценки, назначенное узлу n
g(n) наименьшая стоимость прибытия в узел n из точки старта
h(n) эвристическое приближение стоимости пути к цели от узла n

Таким образом, этот алгоритм сочетает в себе учет длины предыдущего пути из алгоритма Дийкстры с эвристикой из алгоритма "лучший-первый". Алгоритм хорошо отражен в листинге 3. Так как некоторые узлы могут обрабатываться повторно (для поиска оптимальных путей к ним позднее) необходимо ввести новый список Closed для их отслеживания.

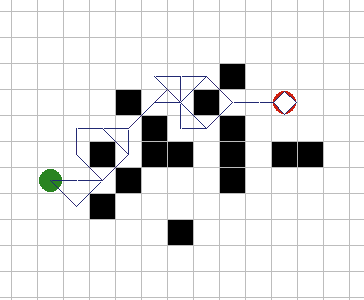
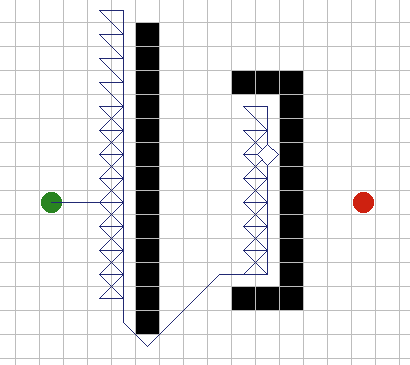
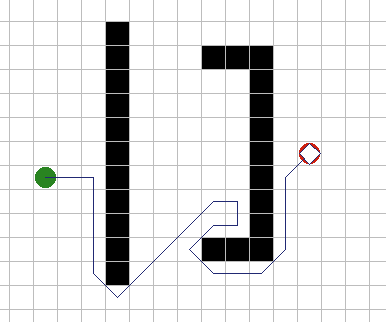
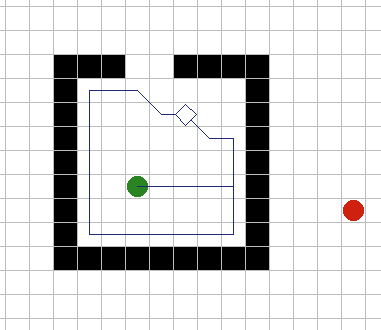
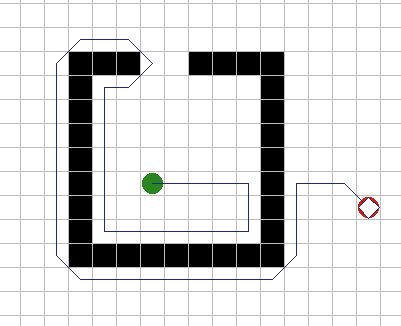
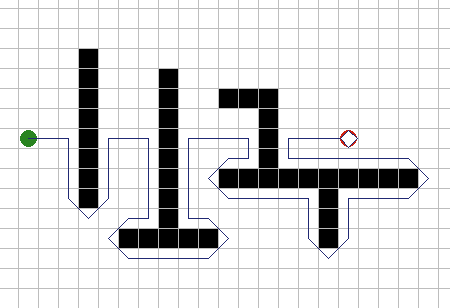
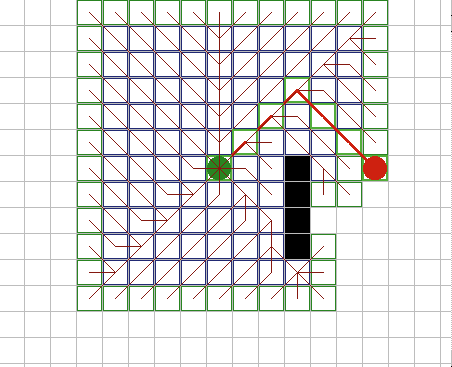
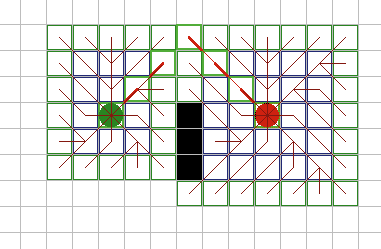
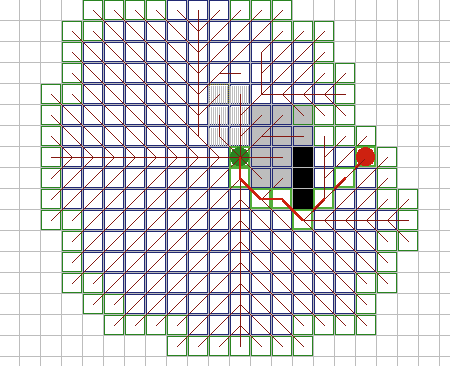
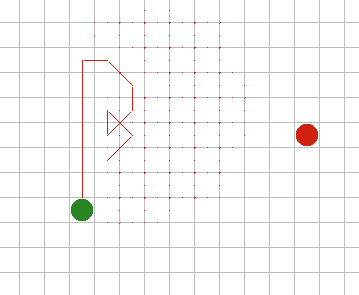
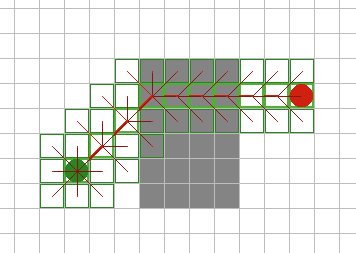
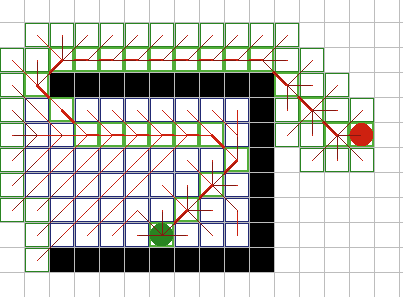
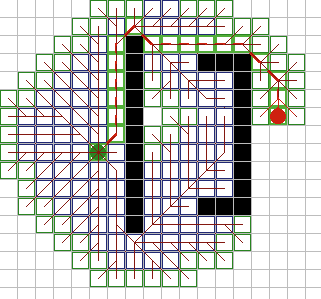
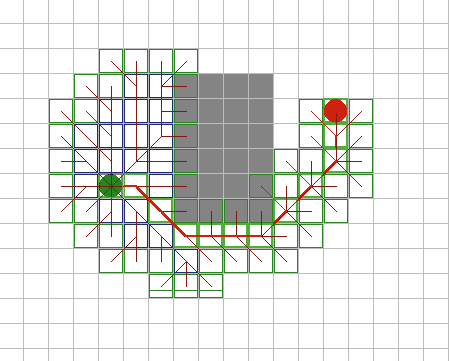
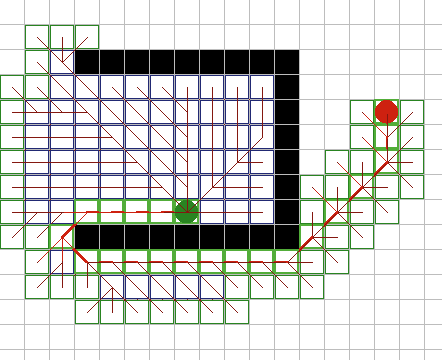
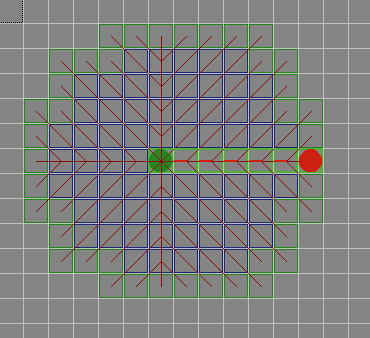
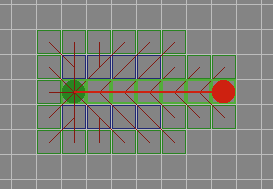
A* имеет множество интересных свойств. Он гарантированно находит кратчайший путь, до тех пор пока эвристическое приближение h(n) является допустимым, то есть он никогда не превышает действительного оставшегося расстояния до цели. Этот алгоритм наилучшим образом использует эвристику: ни один другой алгоритм не раскроет меньшее число узлов, не учитывая узлов с одинаковой стоимостью. На рисунках 9A - 9C, можно увидеть как A* справляется с ситуациями проблемными для других алгоритмов.

Рис. 9А.

Гибкость А*. На практике A* оказывается очень гибким. Рассмотрим различные части алгоритма.

Состоянием зачастую является ячейка или позиция, которую занимает объект. Но при необходимости, состоянием с таким же успехом может быть ориентация и скорость (например, при поиске пути для танка или любой другой машины - их радиус поворота становится хуже при большей скорости).

Соседние состояния могут изменяться в зависимости от игры и локальной ситуации. Смежные позиции могут быть исключены, потому что они непроходимы. Некоторые типы местности могут быть непроходимыми для некоторых объектов, но проходимыми для других; объекты, которые медленно разворачиваются, не могут перемещаться во все соседние клетки.

Стоимость перехода из одной позиции в другую может представлять множество вещей: обычное расстояние между позициями; стоимость по времени или топливу на перемещение; штрафы за проезд через нежелательную область (например, точки в пределах вражеской артиллерии); бонусы за проезд через предпочтительные области (например, исследование новой области или захват контроля над неконтролируемыми зонами); и эстетические соображения (например, если диагональные перемещения такие же по стоимости, как и ортогональные, все равно лучше сделать их стоимость больше, для того чтобы пути выглядели более прямыми и естественными).

Приближение обычно равняется минимальному расстоянию между текущим узлом и целью умноженному на минимальную стоимость передвижения между узлами. Это гарантирует допустимость эвристики h(n). (На карте с квадратными клетками, где объекты могут занимать только точки на сетке, минимальным расстоянием будет не геометрическое расстояние, а минимальное число ортогональных и диагональных перемещений между двумя точками.)

Цель не обязательно должна быть единственной позицией, но может состоять из множества позиций. Тогда приближение должно равняться минимуму приближений ко всем возможным целям. Указание пределов по стоимости пути или по расстоянию, или по обоим признакам может быть легко реализовано. Из моего непосредственного опыта я знаю, что А* хорошо работает для большого числа типов путей в военных играх (wargames) и стратегиях.

Рис. 9Б.

Рис. 9В

Ограничения A*. Существуют ситуации, в которых A* не может работать хорошо по различным причинам. Требования работы в реальном масштабе времени для некоторых игр, плюс ограничения по памяти и процессорному времени в некоторых из них, создают проблемы для хорошей работы даже для А*. Большая карта может требовать тысячи ячеек в списках Open и Closed, для чего может оказаться недостаточно места. Даже если для них окажется достаточно памяти, алгоритмы для работы с этими списками могут оказаться неэффективными.

Качество работы алгоритма сильно зависит от качества эвристического приближения h(n). Если h близко к истинной стоимости оставшегося пути, то эффективность будет очень высокой; с другой стороны, если h будет слишком низким, то это отразится на эффективности в худшую сторону. На самом деле, алгоритм Дийкстры - это A* с h установленной в ноль для всех узлов -это конечно будет допустимым приближением и этот алгоритм найдет путь, но это будет очень медленно. На рисунке 10A, можно увидеть что при поиске в зоне с повышенной стоимостью (затененная зона), фронт просмотренных узлов похож на фронт в алгоритме Дийкстры; на рисунке 10Б при увеличении эвристики стал более сфокусированным.

Рис. 10А

Рис. 10Б

Иерархический поиск. Рассмотрим способы, как добиться от A* большей эффективности в рассматриваемых областях.

Возможно самой главной оптимизацией, которую только можно сделать, является реструктуризация проблемы в более простую. Макрооператоры - это последовательности шагов, которые принадлежат друг другу и могут быть объединены в один шаг, заставляя поиск делать большие шаги за один раз. Например, самолеты делают серию шагов для того, чтобы изменить свои положение и высоту. Общая последовательность может быть использована как одно изменение состояния, вместо множества маленьких отдельных шагов. В дополнение к сказанному, поиск и общие методы решения задач могут быть значительно упрощены, если они будут разбиты на подзадачи, индивидуальное решение каждой из которых довольно простое. В случае поиска пути, карта разбивается на большие непрерывные области, чья связность известна. Выбирается одна или две граничных ячейки, которые находятся между двумя смежными областями; затем поиск производится между смежными областями, в каждой из которых путь находится для граничных ячеек.

Например, в стратегической карте Европы, планировщик пути прокладывающий путь из Мадрида в Афины может с большой вероятностью потратить кучу времени на обработку итальянского "сапога". Используя страны в качестве областей, иерархический планировщик сначала определит, что путь должен следовать из Испании во Францию, затем в Италию, и из Югославии (если смотреть на старую карту) в Грецию; и затем путь через Италию должен вести от границей между Италией и Францией до границы между Италией и Югославией. В качестве другого примера можно привести путь из одной части здания в другое, который может быть разбит на пути между комнатами и коридорами и пути между дверьми в каждой комнате.

Гораздо проще выбирать области в предопределенных картах, чем заставлять делать это компьютер на случайно сгенерированных картах. Необходимо отметить, что обсуждаемые примеры работают в основном с обходом препятствий; для взвешенных областей желательно назначать полезные области, особенно для компьютера (они могут быть и не совсем полезные).

Реализация А* в играх. Хотя поиск А* сам по себе достаточно эффективен, он может быть замедлен неэффективными алгоритмами работы с внутренними структурами данных. Для поиска используются две основных структуры данных.

Первая - это представление игровой области. Тут возникает много вопросов. Как игровая область должна быть представлена? Будут ли области доступны из каждой точки? Стоимости перемещения будут храниться непосредственно в карте или будут вычисляться по необходимости? Как будут представлены различные особенные точки в областях на карте? Будут ли они представлены непосредственно на карте или в отдельных структурах? Как алгоритм поиска может быстро получить необходимую информацию? Ответы на эти вопросы зависят от типа игры и используемого программного и аппаратного обеспечения.

Другая основная используемая структура - это узел или состояние поиска, который можно рассмотреть более детально. На нижнем уровне находится структура состояния поиска, в которую разработчик может захотеть включить следующие поля:

Место (координаты) на карте, рассматриваемое в этом состоянии.
Другие существенные атрибуты объекта, например, ориентация и скорость.
Стоимость лучшего пути к этой позиции из исходной позиции.
Длина пути к этой позиции.
Эвристическое приближение h(n) (стоимости оставшегося пути к цели).
Оценка для этого состояния f(n), используемая для выбора следующего состояния извлекаемого из Open.
Предел длины пути, или его стоимости, или того и другого вместе, если необходимо.
Ссылка (указатель или индекс) на родителя этого узла, то есть узла который привел к этому состоянию.
Дополнительные ссылки на другие узлы, как это требуют структуры хранения данных, используемые для хранения списков Open и Closed; например, "next" и возможно "previous" указатели для связанных списков, "right", "left" и "parent" указатели для двоичных деревьев.

Другим вопросом является решение - когда распределять память под эти структуры? Ответ зависит от требований и ограничений игры, аппаратного обеспечения и операционной системы.

На верхнем уровне находятся более сложные структуры данных - списки Open и Closed. Хотя их раздельное хранение типично, можно хранить их вместе, используя флажок в узле для определения открыт этот узел или нет. Вот виды операций, которые необходимы для работы со списком Closed:

Добавить новый узел.
Удалить произвольный узел.
Искать узел с заданными атрибутами (положение, скорость, направление).
Очистить список в конце поиска.

Для списка Open нужны такие же операции, как для списка Close, плюс:

Извлечь узел с лучшей оценкой f(n).
Изменить оценку узла.

Список Open можно рассматривать как приоритетную очередь, где следующий извлеченный узел является узлом с высшим приоритетом - в нашем случае с наилучшей оценкой. В соответствии с указанными выше операциями есть несколько возможных представлений: линейный, неупорядоченный массив; неупорядоченный связанный список; сортированный массив; сортированный связанный список; куча (структура используемая в heapsort); сбалансированные бинарные деревья. Существует несколько типов бинарных деревьев: 2-3-4 деревья, красно-черные деревья, сбалансированные по глубине (AVL trees), и сбалансированные по весу деревья. Кучи и сбалансированные деревья имеют преимущество логарифмической зависимости времени вставки, удаления и поиска; однако, если количество узлов очень велико, затраты на их хранение могут превысить это преимущество.

Оптимизация А*. Существует несколько способов изменить алгоритм поиска, чтобы получить хорошие результаты при использовании ограниченных ресурсов:

Лучевой поиск. Одним из способов борьбы с ограничением по памяти является наложение ограничений на количество узлов в списке Open; когда список полон и необходимо добавить новый узел, просто выбрасывается узел с наихудшим значением. Список Closed также может быть уничтожен, если каждая ячейка хранит в себе длину наилучшего пути и обратный указатель. Этот алгоритм не гарантирует оптимальности пути, так как узел ведущий к нему может быть выброшен, но все равно может позволить найти разумный путь.

Алгоритм последовательных приближений для A* (IDA*). Алгоритм последовательных приближений, использованный для IDDFS, как упоминалось ранее, может быть использован и для A*. Это полностью избавляет от необходимости хранить списки Open и Closed. Делается простой рекурсивный поиск, собирается наколенная стоимость пути g(n), и поиск прекращается при достижении значением f(n) = g(n) + h(n) заданных пределов. Начинать нужно с пределом остановки равным h(start), и в каждой последовательной итерации, устанавливать новый предел остановки равным минимальному значению f(n), которое превысило прежнюю границу. Аналогично для IDDFS среди методов полного перебора, IDA* - асимптотически оптимален в расходе времени и памяти среди эвристических методов.

Недопустимая эвристика h(n). Как обсуждалось выше, если эвристическое приближение оставшейся стоимости пути слишком мало, то A* может быть очень неэффективным. Но если приближение слишком высоко, то для найденного пути не гарантируется оптимальность. В играх в которых диапазон изменения стоимостей ландшафта широк - от болот до автострад - можно поэкспериментировать с различными промежуточными значениями, чтобы найти точный баланс между эффективностью поиска и качеством найденного пути.

Существуют и другие модификации A*, однако они не подтвердили свою полезность для поиска пути в геометрическом пространстве.

Непрерывное игровое пространство. Все приведенные выше методы поиска предполагали, что пространство разбито на квадратные или шестиугольные ячейки. Но что, если игровое пространство непрерывно? Что, если позиции и объектов и препятствий сохранены в виде непрерывных значений и могут быть настолько точно представлены, как и разрешение экрана? Рисунок 11A показывает примерное расположение объектов. Для ответа на эти условия поиска, можно заглянуть в область робототехники и увидеть какие подходы используются для мобильных роботов. Не удивительно, что многие подходы находят способы для сведения непрерывного пространства к нескольким дискретным вариантам. После этого, они обычно используют A* для поиска желаемого пути. Способы дискретизации пространства включают:

Ячейки. Простым подходом является нанесение ячеистой сетки на поверхность пространства поиска. Ячейки, содержащие часть или все препятствие, обозначаются занятыми; цепочка ячеек, касающихся заблокированных ячеек, также помечаются блокированными для разрешения передвижения без столкновений. Это представление также полезно для проблемы взвешенных областей. (См. рис. 11B.)

Точки видимости. Для проблем обхода препятствий, можно сфокусироваться на критических точках, в основном на расположенных возле вершин препятствий (на достаточном расстоянии, чтобы избежать столкновений), при этом точки считаются соединенными, если они видимы между собой (то есть, между ними нет препятствий). Для любого пути, поиск рассматривает в качестве промежуточных шагов между стартом и целью только критические точки. Смотрите рисунок 11C.

Выпуклые полигоны. Для обхода препятствий, пространство не занимаемое полигональными препятствиями разбивается на выпуклые полигоны; промежуточными точками могут быть центры полигонов или точки на границах полигонов. Существует несколько схем декомпозиции пространства: C-Cells (каждая вершина соединяется с ближайшей видимой вершиной; эти линии разбивают пространство) и разложении на максимальные области (каждая выпуклая вершина препятствия проектирует грани, составляющие вершину, на ближайшие препятствия или стены; из этих двух сегментов и сегмента примыкающего к ближайшей видимой вершине выбирается кратчайший). (См. рис. 11D.) Для проблемы взвешенных областей, пространство разделяется на полигоны с однородной стоимостью проходимости. Точки используемые при пересечении границ вычисляются по закону преломления Снелла. Этот подход избавляет от иррегулярных путей, найденных другими способами.

Квадрантные деревья. Подобно выпуклым полигонам пространство разделяется на квадраты. Каждый квадрат, не являющийся однородным, разделяется на четыре меньших квадрата. Центры этих квадратов используются для поиска пути. (См. рис. 11E.)

Обобщенные цилиндры. Пространство между смежными препятствиями рассматривается как цилиндр, форма которого изменяется вдоль его оси. Вычисляется ось, проходящая через пространство между двумя смежными препятствиями (включая стены), и эти оси используются для поиска пути. (См. рис. 11F.)

Потенциальные поля. Этот подход, не требующий ни квантизации пространства, ни полных предварительных расчетов, считает, что каждое препятствие имеет вокруг себя отталкивающее потенциальное поле, сила которого обратно пропорциональна расстоянию до него; так же существует однородная сила притяжения к цели. Через близкие постоянные интервалы времени вычисляется сумма притягивающих и отталкивающих векторов и объект передвигается в этом направлении. Проблема этого подхода состоит в попадании объекта в локальный минимум; существуют различные способы выезда из таких точек.

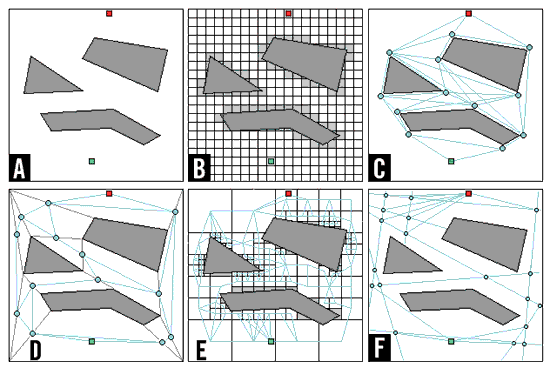
Рис. 11.

Original article © Brian Stout, 1997
Translation into Russian © Maxim Kamensky, 2000
Оригинал перевода и возможные дополнения на skael.nm.ru

Вверх по каталогу, к другим алгоритмам.