Математика: Вычислительная геометрия.

Проверка принадлежности точки многоугольнику.

Случай треугольника.

Для треугольника существует стандартный алгоритм, который надо знать, хотя и более общий тоже годится. Это - 'классика' аналитической геометрии, и в ручных расчетах используется именно он.

char BelongToPoly (point a, point b, point c, point p)

// Определение принадлежности точки треугольнику

{

 float tmp1, tmp2;
 char f1, f2, f3; // Флажки

 /*
    Для определения принадлежности точки 
   треугольнику используется следующий алгоритм:
   вся плоскость делится прямой, содержащей 
   сторону треугольника, на две полуплоскости.
    Далее смотрим, если наша точка и 
   противоположная этой стороне вершина треугольника 
   лежат в разных полуплоскостях, то точка не 
   принадлежит треугольнику.
Такую проверку надо провести для всех 3-х сторон !!!!!
 */

 // Проверяем сторону AB
 // Hаходим её уравнение y(x) по двум точкам
 // Если точка P и точка C лежат в разных полуплоскостях, 
 // то произведение
 // (y(p.x)-p.y)*(y(c.x)-c.y) будет отрицательным
 // Уравнение прямой имеет вид: 
 // y(x)=((x-a.x)*(b.y-a.y))/(b.x-a.x)+a.y

 tmp1=((p.x-a.x)*(b.y-a.y))/(b.x-a.x)+a.y-p.y;
 tmp2=((c.x-a.x)*(b.y-a.y))/(b.x-a.x)+a.y-c.y;
 if (tmp1*tmp2>=0) f1=1;

 // То же проделываем для стороны BC

 tmp1=((p.x-b.x)*(c.y-b.y))/(c.x-b.x)+b.y-p.y;
 tmp2=((a.x-b.x)*(c.y-b.y))/(c.x-b.x)+b.y-a.y;
 if (tmp1*tmp2>=0) f2=1;

 // Аналогично для стороны CA

 tmp1=((p.x-c.x)*(a.y-c.y))/(a.x-c.x)+c.y-p.y;
 tmp2=((b.x-c.x)*(a.y-c.y))/(a.x-c.x)+c.y-b.y;
 if (tmp1*tmp2>=0) f3=1;
// Точка принадлежит
 if ((f1 == 1)&&(f2 == 1)&&(f3 == 1)) return (1); 
 // Точка не принадлежит
 else return (0);                                

}

Выпуклый многоугольник.

Теперь дадим общий алгоритм, пока только для выпуклых многоугольников.

Пусть (x₁,y₁), (x₂,y₂), ... ,(x_n,y_n) - координаты точек полигона на плоскости.

Сразу поясню, что координаты точек заданы в порядке обхода полигона в какую либо (любую) сторону, и стороны полигона не пересекаются (в последнем случае алгоритм тоже может работать корректно, но при дополнительных условиях)

далее в цикле находим знак для каждого из векторных произведений

где Vn - значение в.п. для n-ной пары векторов, а Sign - функция возвращающая знак величины.

Надо отметить, что в этом цикле при n = количеству вершин, n+1 = 1 (я думаю почему - и так понятно).

Что мы делаем в геометрическом смысле ?

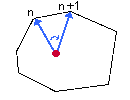Берем пару векторов и 'поворачиваем' их раз за разом на одну точку. Сами векторы меняются, однако кратчайший поворот от n-го к (n+1)-му всегда идет по часовой стрелке, если знак Zn - '+', и против - если минус.

Таким образом, если точка внутри, то знаки всегда будут одинаковы - проверьте сами,
точка снаружи - будет хоть одно несовпадение,
точка на стороне от n к n+1-oй вершине - Z_n=0.

Если же заранее известен обход вершин (например по часовой стрелке), то можно последнее условие упростить: если среди знаков есть '-' (для данного примера), то точка лежит вне, иначе внутри.

Произвольный многоугольник.

С произвольным многоугольником можно поступить гораздо проще, причем алгоритм будет включать и все предыдущие случаи. Проводим горизонтальную прямую через точку и сортируем координаты пересечений со сторонами по x.

Если точка на четном месте - она внутри, на нечетном - снаружи. Отдельно рассматриваем случай нуля и лежит ли точка на пересечении линии со сторонами - иначе могут быть глюки.

Алгоритм гораздо компактнее, но кода придется писать гораздо больше. Не забудьте разобрать случаи, когда точка лежит на сторонах.

Вверх по странице, к оглавлению и навигации.