 |
|
Математика: Быстрое вычисление функций.
Вычисление числа PI.
В 1671 году Джеймс Грегори установил, что: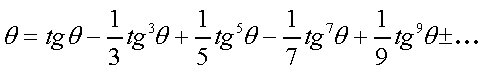
Этот результат позволил Лейбницу получить очень простое выражение для PI, а именно:
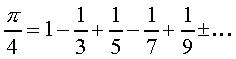
или, после умножения на 4:
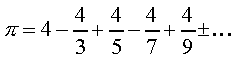
Просуммируйте этот ряд и Вы получите число PI.
Однако, как говорил Козьма Прутков, 'нельзя объять необъятное', что, в применении к данному случаю, можно перефразировать так: нельзя просуммировать бесконечное число слагаемых за конечное время, каким бы быстрым компьютером мы не располагали.
Слава Богу, этого и не требуется. Поскольку мы хотим найти не точное значение PI, а лишь его приближение с пятью верными десятичными знаками, нам достаточно просуммировать такое количество первых членов ряда, чтобы сумма всех оставшихся членов не превышала 10-5.
Остался, правда, открытым вопрос о том, сколько же все-таки членов ряда нужно просуммировать, чтобы получить результат с требуемой точностью?
Ответ на этот вопрос в “общем виде” выходит далеко за рамки настоящего обсуждения. Это отдельная тема в курсах математического анализа и численных методов.
К счастью, данный конкретный ряд позволяет найти очень простое правило, позволяющее определить момент, когда следует прекратить суммирование. Дело в том, что ряд Грегори является знакопеременным и сходится равномерно (хотя и медленнее, чем хотелось бы). Это означает, что для любого нечетного n, сумма первых n членов ряда всегда дает верхнюю оценку для PI, а сумма n+1 первых членов ряда - нижнюю.
Значит, как только разница между верхней и нижней оценками окажется меньше, чем требуемая точность, можно смело прекращать вычисления и быть уверенным, что как та, так и другая оценки отличаются от истинного значения PI не более, чем на 10-5. В качестве окончательного результата разумно взять среднее значение между полученными верхней и нижней оценками. Таким образом, можно предложить алгоритм, приведенный ниже.
- Положить n=0, S1 = 0 и S2 = 0; ( начальные установки )
- Увеличить n на 1; ( n становится нечетным )
- Вычислить S1 = S2 + 4/(2n-1); (S1 - есть верхняя оценка )
- Увеличить n на 1; ( n становится четным )
- Вычислить S2 = S1 - 4/(2n-1); (S2 - есть нижняя оценка)
- Если S1 - S2 >= 10-5 перейти к шагу 2; ( нужная точность еще не достигнута )
- Напечатать результат (S1 + S2) / 2
При реализации этого алгоритма на машине, следует помнить, что ряд Грегори сходится достаточно медленно, и поэтому n может принимать довольно большие значения.
 Вверх по странице, к оглавлению и навигации.
Вверх по странице, к оглавлению и навигации.