Математика: Быстрое вычисление функций.

Числа Фибоначчи за O(logn).

© Кантор. И / Фидо

Идея заключается в следующем.

Можно пользоваться этими формулами в исходном виде, а можно еще подумать:

Имеем матричное уравнение

 | F_n    |        | 1   1 |   | F_(n-2)|
 |        |   =    |       |   |        |
 | F_(n+1)|        | 1   2 |   | F_(n-1)|.

Если через A обозначить матрицу

     | 1   1 |
 A = |       |
     | 1   2 |,

то получаем

 | F_(2n)  |             | 1 |
 |         |   =  A^n *  |   |
 | F_(2n+1)|             | 1 |.

Итак, чтобы вычислить 2n-е/2n+1-е число Фибоначчи, надо матрицу A возвести в n-ую степень, а это можно сделать за O(log n) операций (известный фокус с возведением в квадрат/домножением на A в зависимости от двоичного разложения показателя n).

P.S Мне присылались письма по поводу якобы более простой и успешной формулы n-го члена:

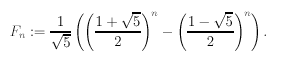
Дело в том, что считать по этой формуле быстрее чем за log n нельзя, так как здесь также есть возведение в n-ю степень. С другой стороны, ошибки округления в этом случае будут колоссальны. Поэтому этой формулой пользоваться НЕ СЛЕДУЕТ.

Вверх по странице, к оглавлению и навигации.