2.8. Рекурсия
Рекурсивное определение процедуры или функции связано с использованием для этого определения самой процедуры или функции. В [2] имеется обоснование того факта, что операции сложения, умножения, возведения в степень, функция факториала, функция предшествования, функция логарифма, показательная функция, квадратный корень, а также полиномы с положительными коэффициентами могут быть реализованы на базе рекурсии. Типичным примером применения механизма рекурсии служит задача вычисления значения факториала ( n! ).
function factorial(n: byte): byte;
begin
if n= 0 then factorial:= 1
else factorial:= factorial( n √ 1 ) * n
end;
Любое рекурсивное описание должно содержать явное определение для некоторых значений аргумента (или аргументов) во избежание порождения бесконечного вычислительного процесса. В примере с факториалом это определение связано с тем, что при нулевом значении аргумента, значение этой функции равно единице.
Для оценки объема рекурсии вводится понятие глубины. Под глубиной рекурсии понимается число промежуточных вычислений функции в процессе ее вычисления для данного аргумента или набора аргументов при условии, что каждое начатое вычисление функции не может быть завершено до окончания начатых позднее вычислений этой функции. Например, при вычислении функции factorial( 3 ) в соответствии с рекурсивным описанием необходимо вычислить factorial( 2 ), factorial( 1 ) и factorial( 0 ), поэтому можно сказать, что здесь рекурсия имеет глубину в три уровня. В примере с функцией factorial глубина рекурсии при любом допустимом значении аргумента очевидна. Это является скорее исключением, чем правилом √ обычно даже для с виду простых описаний функций глубина рекурсии отнюдь не является очевидной. В качестве примера простого описания с неявным показателем глубины рассмотрим алгоритм Евклида для вычисления наибольшего общего делителя двух положительных чисел n и m. Этот алгоритм может быть выражен следующим правилом: если m является точным делителем n, то НОД= m, в противном случае нужно брать функцию НОД от m и от остатка, получаемого при делении n на m. На Pascal это может выглядеть следующим образом:
function nod( n, m: integer ): integer;
begin
if m > n then nod( m, n )
else
if n mod m= 0 then nod:= m
else nod:= nod( m, n mod m )
end;
Хотя это описание является достаточно простым, все же не сразу очевидно, какая глубина рекурсии будет достигнута при вычислении, например, значения nod( 385, 1105 ). Очевидно, что для практических вычислений глубина рекурсии должна быть конечной.
Аспект использования механизма рекурсии состоит, как правило, в повышении уровня простоты и наглядности описания, что приводит к увеличению показателей надежности. Применение рекурсии обосновано в следующих случаях:
1) при работе с рекурсивными структурами данных;
В качестве примера можно привести следующее рекурсивное описание целых чисел без знака:
<целое без знака>::= <цифра> | <целое без знака> <цифра>
<цифра>::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
Синтаксический анализ цепочки на предмет соответствия данному описанию может быть сведен к процессу распознавания с глубиной рекурсии, зависящей от количества цифр в исходной цепочке. Например, для цепочки ▒123' глубина рекурсии равнялась бы трем (с этапами 123 √ целое без знака, за которым следует цифра 3; 12 √ целое без знака 1, за которым следует цифра 2; 1- цифра).
2) при реализации процесса, имеющего рекурсивную природу (например, в таких, как factorial и nod, рассмотренных выше). В остальных случаях, то есть при обработке не существенно рекурсивных по своей природе структур данных и процессов, целесообразна четкая оценка прерогатив быстродействия и надежности.
Существует явная рекурсия, в рамках которой обращение к процедуре или функции содержится в ее теле и неявная, которая связана с наличием обращения к данной процедуре или функции в той процедуре или функции, вызов которой осуществляется из данной.
Реализация механизма рекурсии состоит в формировании копии информационной среды для каждого вызова рекурсивной процедуры и функции. Например, при вызове функции f с фактическим параметром n= 3 будут сформированы следующие копии переменной n▓= 2, n▓▓= 1, n▓▓▓= 0:
f( 3 ) √ f( 2 ) * 3 √ f( 1 ) * 2 * 3 √ f( 0 ) * 1 * 2 * 3 √ 6
n n▓ n▓▓ n▓▓▓
При этом, должна существовать та копия, которая не будет себя копировать (в примере n▓▓▓= 0), а передает управление предыдущей копии и т. д. Из этого следует, что во избежание бесконечной рекурсии следует обращать внимание на задание условия выхода из рекурсивного процесса (в данном примере n= 0).
Разберем решение типичной задачи, связанной с использованием механизма рекурсии.
Текст задания
Во входном файле записана (без ошибок) формула следующего вида:
<формула>::= <цифра>|(<формула><знак><формула>)
<знак>::= +|-|*
<цифра>::= 0|1|2|3|4|5|6|7|8|9
Вывести эту формулу и вычислить ее значение.(Например, ((1-2)*4): -4.)
Решение
program formula;
var
Source: file of char;
function F: integer;
{F читает из начала входного файла литеры, образующие законченную формулу, и вычисляет ее значение как целое}
var
c, op: char;
x, y: integer;
begin
read( Source, c );
if ( c >= '0' ) and ( c <= '9' ) then
{цифра есть формула}
F:= ord( c ) - ord( '0' )
else begin
{началась формула вида (x op y)}
x:= F;
read( Source, op );
y:= F;
case op of
'+': F:= x + y;
'-': F:= x - y;
'*': F:= x * y
end;
read( Source, c ) {пропуск ▒)▓}
end
end; {of F}
begin
assign( Source, 'c:\temp\source.txt' );
reset( Source );
writeln( F );
close( Source )
end.
Варианты заданий
1. Задача о 8 ферзях: на шахматной доске расставить 8 ферзей так, чтобы они "не били" друг друга. Написать программу, которая печатает одну из таких расстановок.
2. Задача о 8 ферзях: на шахматной доске расставить 8 ферзей так, чтобы они "не били" друг друга. Написать программу, которая печатает все 92 такие расстановки.
3. Дано n различных натуральных чисел (n=5). Напечатать все перестановки этих чисел.
4. Имеется n населенных пунктов, перенумерованных от 1 до n (n=10). Некоторые пары пунктов соединены дорогами. Определить, можно ли по этим дорогам попасть из 1-го пункта в n-й. Информация о дорогах задается в виде последовательности пар чисел i и j (i < j), указывающих, что i-й и j-й пункты соединены дорогой; признак конца этой последовательности - пара нулей.
5. (╚Ханойские башни╩). Имеются три колышка А ,В и С и n дисков разного размера, перенумерованных от 1 до n в порядке возрастания их размеров. Сначала все диски надеты на колышек А. Требуется перенести все диски с колышка А на колышек С, соблюдая при этом следующее условия: диски можно переносить только по одному, больший диск нельзя ставить на меньший. Написать программу, которая печатает последовательность действий (в виде "перенести диск с q на r " , где q и r - А , В или С ), решающую указанную задачу для n дисков, где n - заданное натуральное число.
6. Во входном файле задан текст, за которым следует точка. Проверить удовлетворяет ли его структура следующему определению:
<текст >:: = <элемент > | <элемент > < текст >
<элемент >::= a | b | (<текст >) | [<текст >] | {<текст >}
7. Во входном файле записано без ошибок логическое выражение следующего вида:
<логическое выражение>::= true | false | <операция> ( <операнды > )
<операция >::= not | and | or
<операнды>::= <операнд> | <операнд>, <операнды>
<операнд>::= <логическое выражение >
(У операций and и or может быть любое число операндов, у not - только один.) Ввести это выражение и вычислить его значение .(Например, and (or (false ,not (false)),true,not (true)): false)
8. Во входном файле задан текст, за которым следует точка. Проверить, является ли этот текст правильной записью формулы следующего вида:
<формула>::= <цифра> | (<формула> <знак> <формула>)
<знак>::= + | - | *
<цифра>::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
9. Дана последовательность ненулевых целых чисел, за которой следует 0. Напечатать сначала все отрицательные числа этой последовательности, а затем - все положительные (в любом порядке).
10. Напечатать в обратном порядке заданный во входном файле текст (за текстом следует точка).
11. Описать рекурсивную функцию digits без параметров, которая подсчитывает количество цифр в тексте, заданном во входном файле (за текстом следует точка).
12. Во входном файле заданна непустая последовательность положительных вещественных чисел, за которой следует отрицательное число. Описать рекурсивную функцию sum без параметров для нахождения суммы этих положительных чисел.
13. type строка = packed array [1..100] of char; Описать рекурсивную логическую функцию sim( s, i, j ), проверяющую, является ли симметричной часть строки s, начинающаяся i-м и кончающаяся j -м ее элементами.
14. const n=40; type vector =array [1..n] of real; Описать функцию min ( x ) для определения минимального элемента вектора x, введя вспомогательную рекурсивную функцию min1( k ), находящую минимум среди последних элементов вектора x, начиная с k-го.
15. Описать рекурсивную функцию root (f, a, b, eps), которая методом деления отрезка пополам находит с точностью eps корень уравнения f(x)=0 на отрезке (a, b). (Cчитать, что eps > 0 ,a < b, f(a)*f(b) < 0 и f(x) -непрерывная и монотонная функция на отрезке (a, b).)
16. Рекурсивно описать функцию C(m, n) где 0<=m<=n ,т для биноминального коэффициента Сn по следующей формуле :
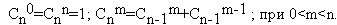
17. Описать рекурсивную функцию pow(x, n) от вещественного x (x <> 0) и целого n , которая вычисляет величину xn согласно формуле
X^n= 1, при n= 0
X^n= 1/ X^|n|, при n < 0
X^n= X*X^(n-1) 1, при n > 0
18. type name= (George, Alex, Piter, Ann, Paul, John, Fred, Natalie, Robert); family= (son, daugther, father, mother, no); Предполагая уже описанными функции father(x) и mother(x), значениями которых являются имена соответственно отца и матери человека по имени x или идентификатор no, если отсутствуют сведения о соответствующем родителе, описать логическую функцию child(a, b) проверяющую является ли человек с именем b потомком (ребенком, внуком, правнуком, и т.п.) человека с именем a.
19. type name= (George, Alex, Piter, Ann, Paul, John, Fred, Natalie, Robert); family= (son, daugther, father, mother, no); Предполагая уже описанными функции father(x) и mother(x), значениями которых являются имена соответственно отца и матери человека по имени x или идентификатор no, если отсутствуют сведения о соответствующем родителе, описать логическую функцию child(a, b) проверяющую является ли человек с именем b потомком (ребенком, внуком, правнуком, и т.п.) человека с именем a. Решить данную задачу в предположении, что имеется функция childcount(x), указывающее число детей человека с именем x, и функция ischild(x, k), указывающая имя k-го ребенка человека с именем x (k не должно превышать число детей человека x).
20. Вычислить определитель заданной квадратной матрицы A n-го порядка (n= 15), используя формулу разложения по первой строке
-матрица, полученная удалением 1-й строки и k-го столбца. (Рекомендация: определить рекурсивную функцию от параметров l и s, которая по указанной формуле вычисляет определитель матрицы, полученной из A удалением первых l строк и всех столбцов, номера которых принадлежат множеству s.)
21. Дан некоторый текст, за которым следует точка (в сам текст точка не входит). Определить, является ли этот текст правильной записью формулы:
<формула>::= <терм> | ( <формула> <знак> <формула> )
<знак>::= + | - | *
<терм>::= <имя> | <целое>
<имя>::= <буква> | <имя> <буква> | <имя> <цифра>
<целое>::= <цифра> | <целое> <цифра>
<буква>::= а | б | в | г | д | е | ж
<цифра>::= 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
22. Описать рекурсивную функцию digits1 без параметров, которая подсчитывает количество символов ▒+▓, ▒-▒, ▒*▓ в тексте, заданном во входном файле (за текстом следует точка).
23. Во входном файле заданна непустая последовательность положительных вещественных чисел, за которой следует отрицательное число. Описать рекурсивную функцию sum1 без параметров для нахождения произведения этих положительных чисел.
24. const n=100; type vector =array [1..n] of real; Описать функцию max ( x ) для определения максимум элемента вектора x, введя вспомогательную рекурсивную функцию max1( k ), находящую максимум среди последних элементов вектора x, начиная с k-го.
25. Описать рекурсивную функцию digits1 без параметров, которая подсчитывает количество символов гласных букв в тексте, заданном во входном файле (за текстом следует точка) и состоящем из строчных латинских букв.
26. Описать рекурсивную функцию digits2 без параметров, которая подсчитывает количество символов согласных букв в тексте, заданном во входном файле (за текстом следует точка) и состоящем из строчных латинских букв.
27. Из текстового файла, состоящего из строчных латинских букв вывести сначала все гласные буквы, затем все согласные.
28. Во входном файле задан текст, за которым следует точка. Проверить, является ли этот текст правильной записью отношения следующего вида:
<отношение>::= <число> <знак отношения> <число>
<знак отношения>::= < | = | > | <= | <> | >=
<число>::= <цифра> | <цифры>
<цифры>::= <неноль> <цифра> | <цифры> <цифра>
<неноль>::= 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9
<цифра>::= 0 | <неноль>
29. Заданный вещественный массив из n различных элементов (n = 100) упорядочить по возрастанию следующим методом быстрой сортировки: выбрать какой-нибудь (например, средний) элемент массива и переставить элементы массива так, чтобы слева от выбранного элемента оказались только меньшие элементы, а справа √ только большие (тем самым выбранный элемент окажется на своем месте), после чего рекурсивно применить этот же метод к левой и правой частям массива.
30. Из заданного текстового файла вывести сначала все цифры, затем все буквы латинского алфавита, наконец, все оставшееся символы.